Friday, February 28

You can also download a PDF copy of this lecture.

Poisson Regression for Rates

The $i$ -th observed rate $R_i$ can be written as $R_i = C_i/S_i,$ where $C_i$ is a count and $S_i$ is the “size” of the interval in which the counts are observed. Examples include fish per minute, epileptic episodes per day, or defects per (square) meter. In some cases $S_i$ is referred to as the “exposure” of the $i$ -th observation.

Assume that the count $C_i$ has a Poisson distribution and that $E(C_i) = S_i \underbrace{\exp(\beta_0 + \beta_1 x_{i1} + \cdots + \beta_k x_{ik})}_{\lambda_i},$ where $\lambda_i$ is the expected count per unit (e.g., per minute) so that $S_i\lambda_i$ is then the expected count per $S_i$ (e.g., per hour if $S_i$ = 60, per day if $S_i$ = 1440, or per second if $S_i$ = 1/60). The expected rate is then $E(R_i) = E(C_i/S_i) = E(C_i)/S_i = \exp(\beta_0 + \beta_1 x_{i1} + \cdots + \beta_k x_{ik}),$ if we treat exposure as fixed (like we do $x_{i1}, x_{i2}, \dots, x_{ik}$ ). But rather than using $R_i$ as the response variable we can use $C_i$ as the response variable in a Poisson regression model where $E(C_i) = S_i \exp(\beta_0 + \beta_1 x_{i1} + \cdots + \beta_k x_{ik}) = \exp(\beta_0 + \beta_1 x_{i1} + \cdots + \beta_k x_{ik} + \log S_i),$ and where $\log S_i$ is an “offset” variable (i.e., basically an explanatory variable where it’s $\beta_j$ is “fixed” at one).

Note: If $S_i$ is a constant for all observations so that $S_i = S$ then we can write the model as $E(C_i) = \exp(\beta_0 + \beta_1 x_{i1} + \cdots + \beta_k x_{ik} + \log S_i) = \exp(\beta_0^* + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_k x_{ik}),$ where $\beta_0^* = \log(S) + \beta_0$ so that the offset is “absorbed” into $\beta_0$ , and we do not need to be concerned about it. Including an offset is only necessary if $S_i$ is not the same for all observations.

Variance of Rates

Using rates as response variables in a linear or nonlinear model without accounting for $S_i$ is not advisable because of heteroscedasticity due to unequal $S_i$ .

We have that $E(R_i) = E(C_i)/S_i$ . But $\mbox{Var}(R_i) = \mbox{Var}(C_i/S_i) = \mbox{Var}(C_i)/S_i^2 = E(R_i)S_i/S_i^2 = E(R_i)/S_i,$ because (a) $\mbox{Var}(Y/c) = \mbox{Var}(Y)/c^2$ if $c$ is a constant, $\mbox{Var}(C_i) = E(C_i)$ because $C_i$ has a Poisson distribution, and thus $E(C_i) = E(R_i)S_i$ . Thus the variance of the rate depends on the expected response and $S_i$ (so larger/smaller $S_i$ , then smaller/larger variance of $R_i)$ .

We can deal with this heteroscedasticity by either (a) using an appropriate offset variable in Poisson regression or a related model or (b) using weights of $w_i = S_i/E(R_i)$ in an iteratively weighted least squares with weights of $w_i = S_i/\hat{y}_i$ .

Modeling Rates with Poisson Regression

Software for GLMs (and sometimes linear models) will often permit specification of an offset variable. In R this is done using offset in the model formula.

Example: Consider the following data from an observational study of auto accidents.

library(trtools)
head(accidents)

  accidents years location treatment
1        13     9        a    before
2         6     9        b    before
3        30     8        c    before
4        20     8        d    before
5        10     9        e    before
6        15     8        f    before

p <- ggplot(accidents, aes(x = location, y = accidents/years)) +
  geom_point(aes(size = years, color = treatment)) + 
  labs(x = "Location", y = "Accidents per Year", 
    size = "Years", color = "Treatment") + theme_minimal()
plot(p)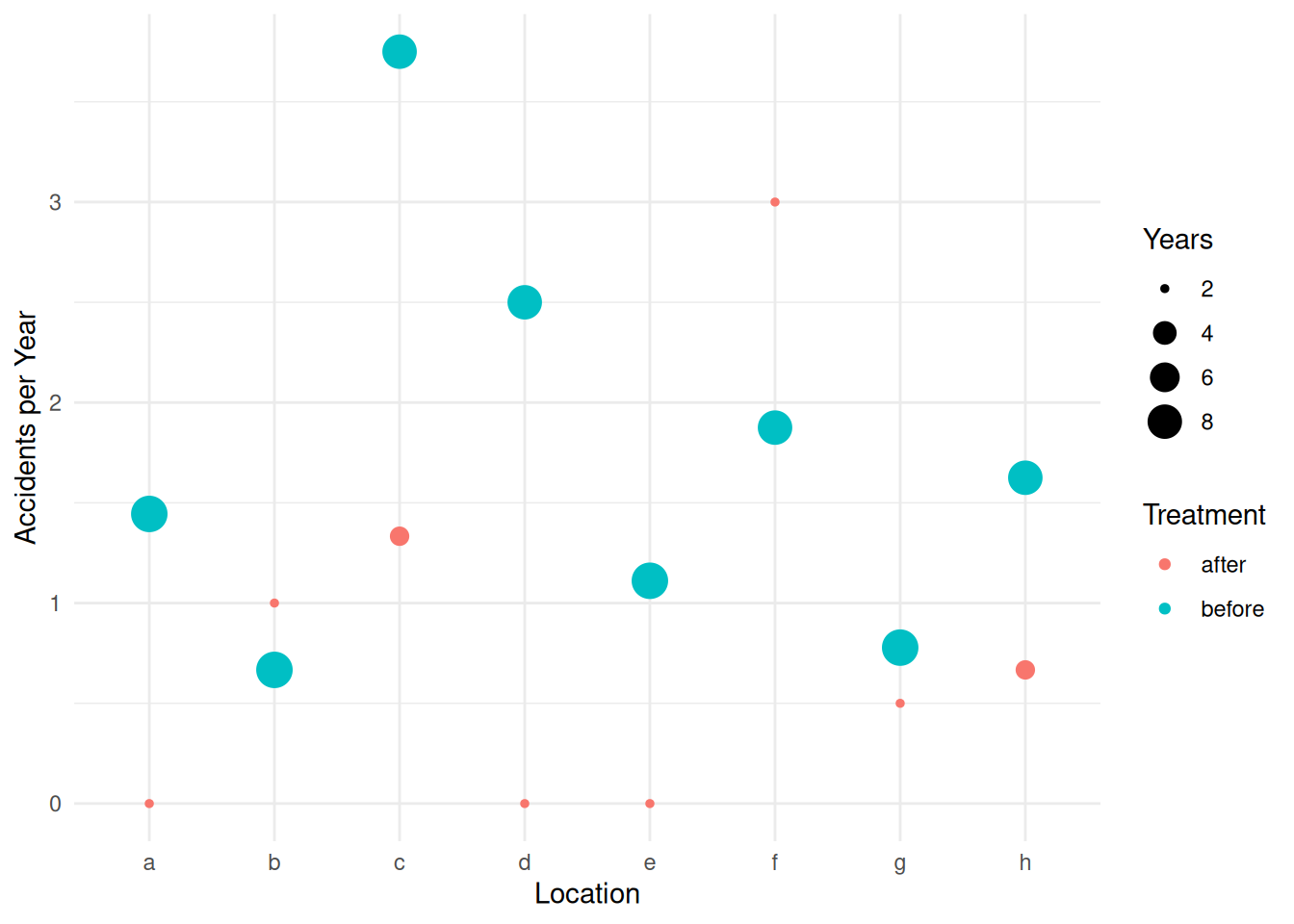

m <- glm(accidents ~ location + treatment + offset(log(years)), 
  data = accidents, family = poisson)
cbind(summary(m)$coefficients, confint(m))

                Estimate Std. Error z value Pr(>|z|)   2.5 % 97.5 %
(Intercept)       -0.510      0.373  -1.366  0.17207 -1.2924  0.177
locationb         -0.486      0.449  -1.080  0.27994 -1.4122  0.378
locationc          1.018      0.326   3.117  0.00182  0.4027  1.694
locationd          0.537      0.356   1.507  0.13168 -0.1510  1.260
locatione         -0.262      0.421  -0.624  0.53279 -1.1136  0.559
locationf          0.586      0.353   1.660  0.09690 -0.0939  1.304
locationg         -0.486      0.449  -1.080  0.27994 -1.4122  0.378
locationh          0.199      0.379   0.526  0.59921 -0.5459  0.958
treatmentbefore    0.781      0.275   2.834  0.00459  0.2741  1.362

exp(cbind(coef(m), confint(m)))

                      2.5 % 97.5 %
(Intercept)     0.601 0.275   1.19
locationb       0.615 0.244   1.46
locationc       2.767 1.496   5.44
locationd       1.711 0.860   3.53
locatione       0.769 0.328   1.75
locationf       1.797 0.910   3.68
locationg       0.615 0.244   1.46
locationh       1.221 0.579   2.61
treatmentbefore 2.183 1.315   3.90

When using other tools like contrast or functions from the emmeans package, be sure to specify the offset. Typically we would use a value of one corresponding to one unit of whatever the offset represents (e.g., space or time). Here are the rate ratios for the treatment.

trtools::contrast(m,
  a = list(treatment = "before", location = letters[1:8], years = 1),
  b = list(treatment = "after", location = letters[1:8], years = 1),
  cnames = letters[1:8], tf = exp)

  estimate lower upper
a     2.18  1.27  3.75
b     2.18  1.27  3.75
c     2.18  1.27  3.75
d     2.18  1.27  3.75
e     2.18  1.27  3.75
f     2.18  1.27  3.75
g     2.18  1.27  3.75
h     2.18  1.27  3.75

trtools::contrast(m,
  a = list(treatment = "after", location = letters[1:8], years = 1),
  b = list(treatment = "before", location = letters[1:8], years = 1),
  cnames = letters[1:8], tf = exp)

  estimate lower upper
a    0.458 0.267 0.786
b    0.458 0.267 0.786
c    0.458 0.267 0.786
d    0.458 0.267 0.786
e    0.458 0.267 0.786
f    0.458 0.267 0.786
g    0.458 0.267 0.786
h    0.458 0.267 0.786

Here are the estimated expected number of accidents per year at location a.

trtools::contrast(m, a = list(treatment = c("before","after"), location = "a", years = 1),
  cnames = c("before","after"), tf = exp)

       estimate lower upper
before    1.311 0.759  2.26
after     0.601 0.289  1.25

Here are the estimated expected number of accidents per decade at location a.

trtools::contrast(m, a = list(treatment = c("before","after"), location = "a", years = 10),
  cnames = c("before","after"), tf = exp)

       estimate lower upper
before    13.11  7.59  22.6
after      6.01  2.89  12.5

When using functions from the emmeans package we use the offset argument with the value specified on the log scale. Here are the estimated number of accidents per decade.

library(emmeans)
emmeans(m, ~treatment|location, type = "response", offset = log(10))

location = a:
 treatment rate   SE  df asymp.LCL asymp.UCL
 after      6.0 2.24 Inf      2.89      12.5
 before    13.1 3.65 Inf      7.59      22.6

location = b:
 treatment rate   SE  df asymp.LCL asymp.UCL
 after      3.7 1.60 Inf      1.58       8.6
 before     8.1 2.86 Inf      4.03      16.2

location = c:
 treatment rate   SE  df asymp.LCL asymp.UCL
 after     16.6 4.83 Inf      9.39      29.4
 before    36.3 6.39 Inf     25.68      51.2

location = d:
 treatment rate   SE  df asymp.LCL asymp.UCL
 after     10.3 3.42 Inf      5.35      19.7
 before    22.4 5.06 Inf     14.42      34.9

location = e:
 treatment rate   SE  df asymp.LCL asymp.UCL
 after      4.6 1.86 Inf      2.10      10.2
 before    10.1 3.20 Inf      5.42      18.8

location = f:
 treatment rate   SE  df asymp.LCL asymp.UCL
 after     10.8 3.56 Inf      5.65      20.6
 before    23.6 5.18 Inf     15.30      36.3

location = g:
 treatment rate   SE  df asymp.LCL asymp.UCL
 after      3.7 1.60 Inf      1.58       8.6
 before     8.1 2.86 Inf      4.03      16.2

location = h:
 treatment rate   SE  df asymp.LCL asymp.UCL
 after      7.3 2.56 Inf      3.70      14.5
 before    16.0 4.18 Inf      9.59      26.7

Confidence level used: 0.95 
Intervals are back-transformed from the log scale

Here is the rate ratio for the effect of treatment.

pairs(emmeans(m, ~treatment|location, type = "response", offset = log(10)), infer = TRUE)

location = a:
 contrast       ratio    SE  df asymp.LCL asymp.UCL null z.ratio p.value
 after / before 0.458 0.126 Inf     0.267     0.786    1  -2.834  0.0046

location = b:
 contrast       ratio    SE  df asymp.LCL asymp.UCL null z.ratio p.value
 after / before 0.458 0.126 Inf     0.267     0.786    1  -2.834  0.0046

location = c:
 contrast       ratio    SE  df asymp.LCL asymp.UCL null z.ratio p.value
 after / before 0.458 0.126 Inf     0.267     0.786    1  -2.834  0.0046

location = d:
 contrast       ratio    SE  df asymp.LCL asymp.UCL null z.ratio p.value
 after / before 0.458 0.126 Inf     0.267     0.786    1  -2.834  0.0046

location = e:
 contrast       ratio    SE  df asymp.LCL asymp.UCL null z.ratio p.value
 after / before 0.458 0.126 Inf     0.267     0.786    1  -2.834  0.0046

location = f:
 contrast       ratio    SE  df asymp.LCL asymp.UCL null z.ratio p.value
 after / before 0.458 0.126 Inf     0.267     0.786    1  -2.834  0.0046

location = g:
 contrast       ratio    SE  df asymp.LCL asymp.UCL null z.ratio p.value
 after / before 0.458 0.126 Inf     0.267     0.786    1  -2.834  0.0046

location = h:
 contrast       ratio    SE  df asymp.LCL asymp.UCL null z.ratio p.value
 after / before 0.458 0.126 Inf     0.267     0.786    1  -2.834  0.0046

Confidence level used: 0.95 
Intervals are back-transformed from the log scale 
Tests are performed on the log scale

Use reverse = TRUE to “flip” the rate ratio. Also for rate ratios the size of the offset does not matter since it “cancels-out” in the ratio. Also since there is no interaction in this model which means the rate ratio does not depend on location, we can omit it when using emmeans (but not contrast).

pairs(emmeans(m, ~treatment, type = "response"), infer = TRUE)

 contrast       ratio    SE  df asymp.LCL asymp.UCL null z.ratio p.value
 after / before 0.458 0.126 Inf     0.267     0.786    1  -2.834  0.0046

Results are averaged over the levels of: location 
Confidence level used: 0.95 
Intervals are back-transformed from the log scale 
Tests are performed on the log scale

When using predict we need to be sure to also include the offset amount. Again, we would use a value of one assuming we want the number of events per unit space/time.

d <- expand.grid(treatment = c("before","after"), location = letters[1:8], years = 1)
d$yhat <- predict(m, newdata = d, type = "response")
head(d)

  treatment location years  yhat
1    before        a     1 1.311
2     after        a     1 0.601
3    before        b     1 0.807
4     after        b     1 0.370
5    before        c     1 3.627
6     after        c     1 1.662

p <- ggplot(accidents, aes(x = location, y = accidents/years)) +
  geom_point(aes(size = years, color = treatment)) + 
  labs(x = "Location", y = "Accidents per Year", 
    size = "Years", color = "Treatment") + theme_minimal() + 
  geom_point(aes(y = yhat, color = treatment), data = d) + 
  geom_line(aes(y = yhat, group = treatment, color = treatment), data = d)
plot(p)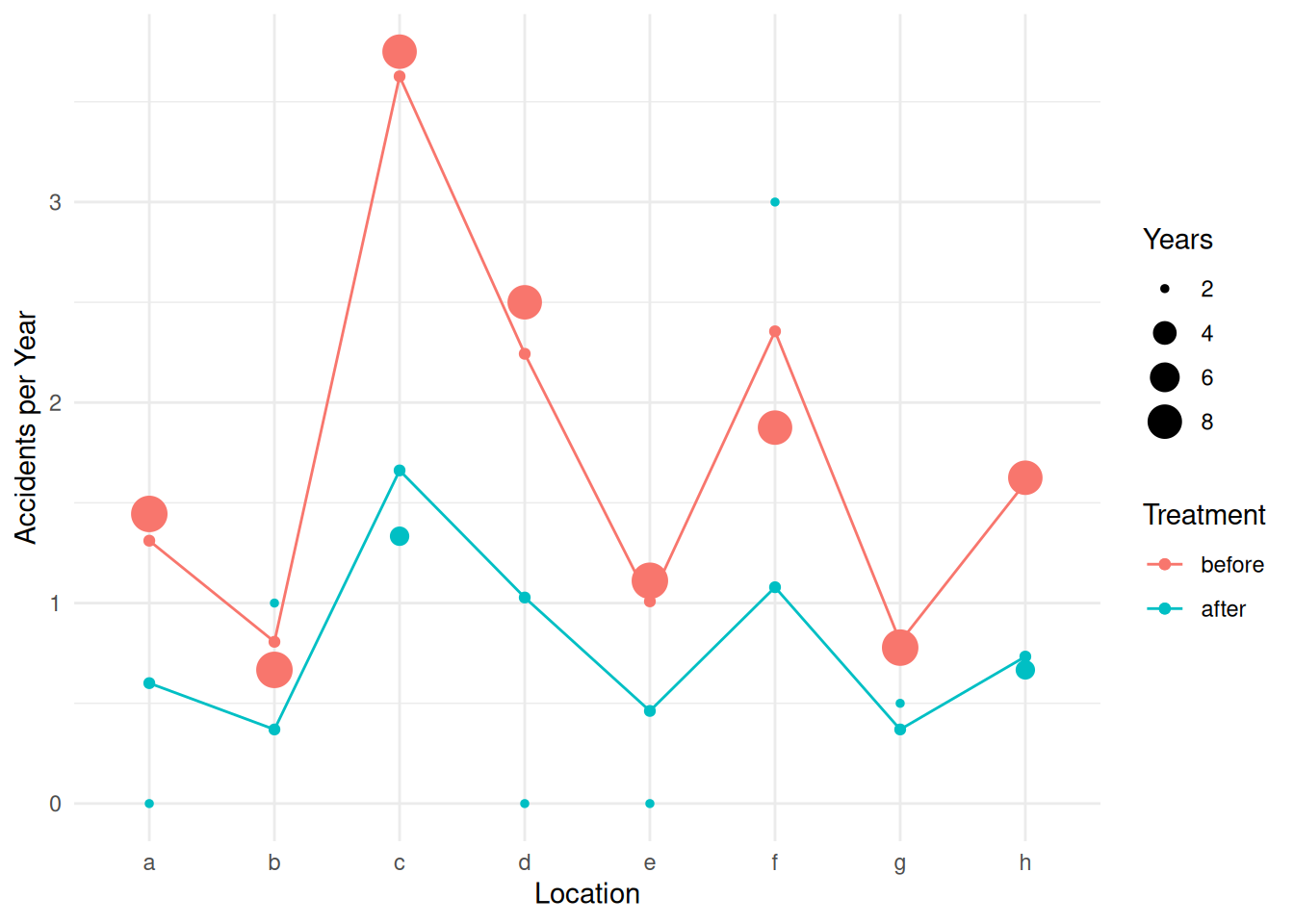

We can use the glmint function from the trtools package if we want to produce confidence intervals for plots.

d <- expand.grid(treatment = c("before","after"), location = letters[1:8], years = 1)
d$yhat <- predict(m, newdata = d, type = "response")
glmint(m, newdata = d)

     fit   low   upp
1  1.311 0.759 2.263
2  0.601 0.289 1.248
3  0.807 0.403 1.616
4  0.370 0.158 0.864
5  3.627 2.568 5.123
6  1.662 0.939 2.939
7  2.243 1.442 3.489
8  1.028 0.535 1.975
9  1.008 0.542 1.878
10 0.462 0.210 1.018
11 2.355 1.530 3.625
12 1.079 0.565 2.059
13 0.807 0.403 1.616
14 0.370 0.158 0.864
15 1.600 0.959 2.671
16 0.733 0.370 1.453

cbind(d, glmint(m, newdata = d))

   treatment location years  yhat   fit   low   upp
1     before        a     1 1.311 1.311 0.759 2.263
2      after        a     1 0.601 0.601 0.289 1.248
3     before        b     1 0.807 0.807 0.403 1.616
4      after        b     1 0.370 0.370 0.158 0.864
5     before        c     1 3.627 3.627 2.568 5.123
6      after        c     1 1.662 1.662 0.939 2.939
7     before        d     1 2.243 2.243 1.442 3.489
8      after        d     1 1.028 1.028 0.535 1.975
9     before        e     1 1.008 1.008 0.542 1.878
10     after        e     1 0.462 0.462 0.210 1.018
11    before        f     1 2.355 2.355 1.530 3.625
12     after        f     1 1.079 1.079 0.565 2.059
13    before        g     1 0.807 0.807 0.403 1.616
14     after        g     1 0.370 0.370 0.158 0.864
15    before        h     1 1.600 1.600 0.959 2.671
16     after        h     1 0.733 0.733 0.370 1.453

d <- cbind(d, glmint(m, newdata = d))
p <- ggplot(accidents, aes(x = location)) + 
  geom_point(aes(y = accidents/years, size = years), shape = 21, fill = "white") + 
  facet_wrap(~ treatment) + theme_minimal() + 
  labs(x = "Location", y = "Accidents per Year", size = "Years") + 
  geom_errorbar(aes(ymin = low, ymax = upp), data = d, width = 0.5) + 
  geom_point(aes(y = fit), data = d)
plot(p)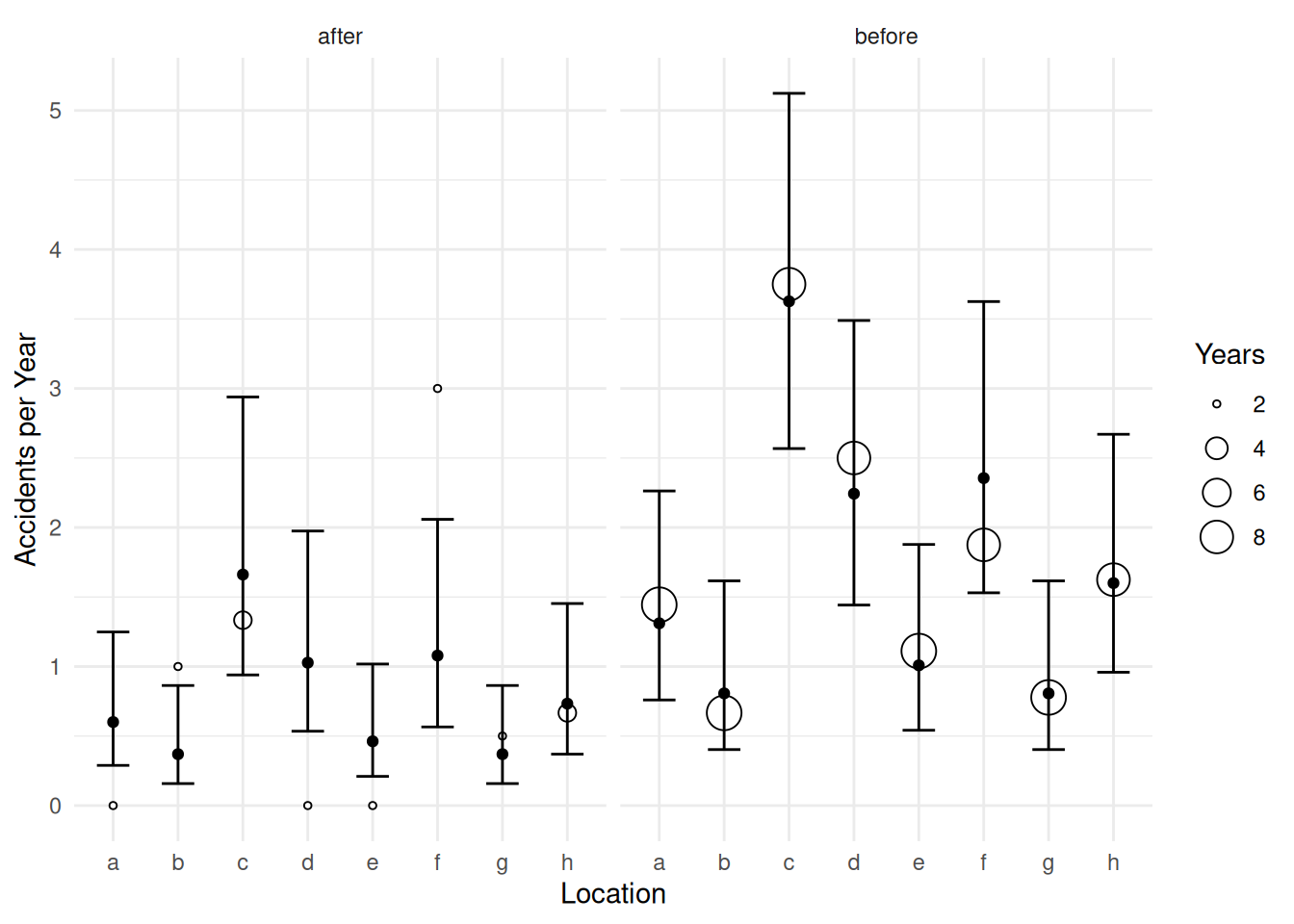

p <- ggplot(accidents, aes(x = location, color = treatment)) + 
  geom_point(aes(y = accidents/years, size = years), 
    position = position_dodge(width = 0.6), shape = 21, fill = "white") + 
  labs(x = "Location", y = "Accidents per Year", 
    size = "Years", color = "Treatment") + theme_minimal() + 
  geom_errorbar(aes(ymin = low, ymax = upp), data = d, 
    position = position_dodge(width = 0.6), width = 0.5) + 
  geom_point(aes(y = fit), data = d, position = position_dodge(width = 0.6))
plot(p)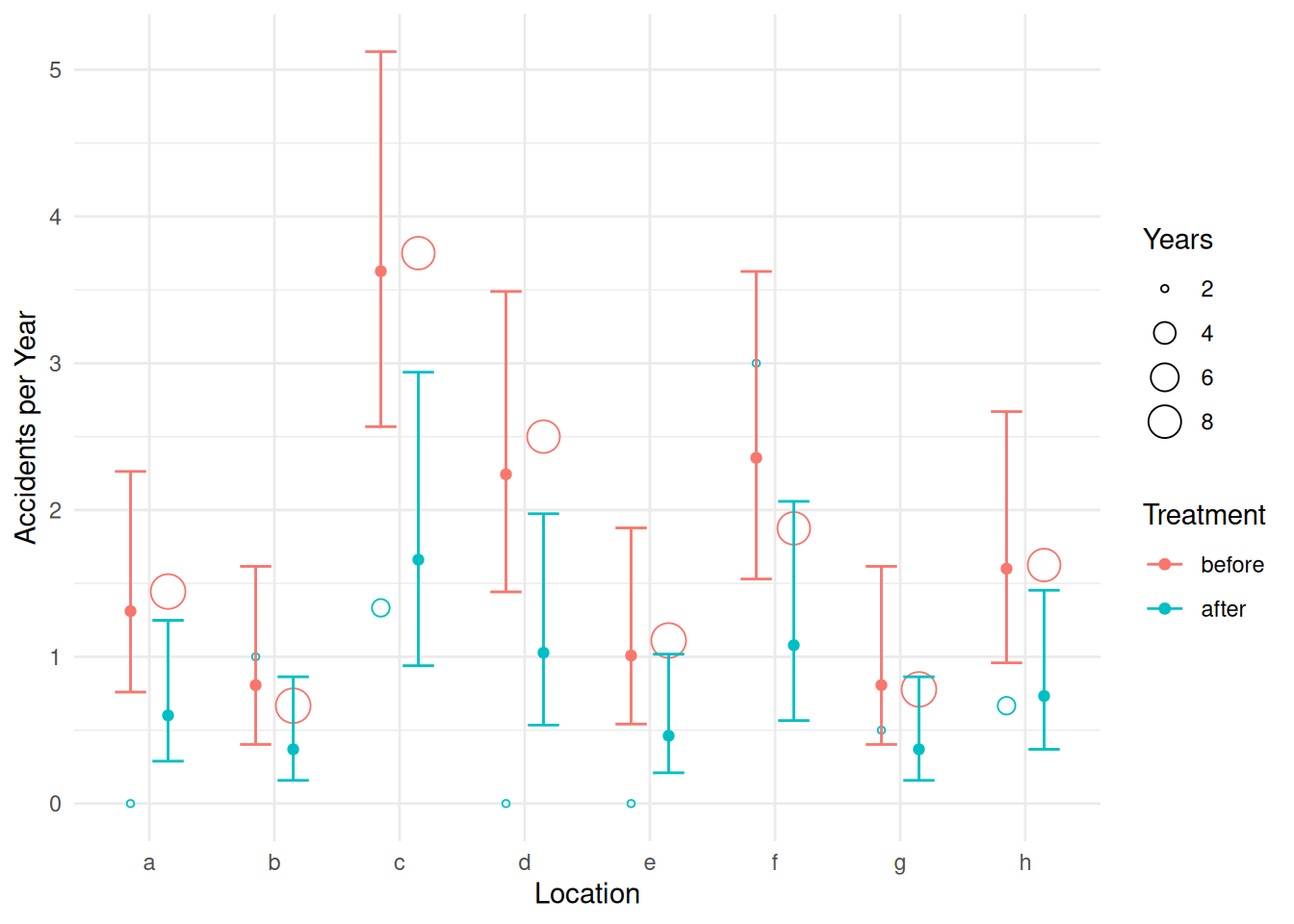

Example: Consider the following data from an observational study that investigated the possible effect of the development of a commercial fishery on deep sea fish abundance. The figure below shows the number of fish per square meter of swept area from 147 trawls by mean depth in meters, and by whether the trawl was during one of two periods. The 1977-1989 period was from before the development of a commercial fishery, and the period 2000-2002 was when the fishery was active.

library(COUNT)
data(fishing)
head(fishing)

  site totabund  density meandepth year    period sweptarea
1    1       76 0.002070       804 1978 1977-1989     36710
2    2      161 0.003520       808 2001 2000-2002     45741
3    3       39 0.000981       809 2001 2000-2002     39775
4    4      410 0.008039       848 1979 1977-1989     51000
5    5      177 0.005933       853 2002 2000-2002     29831
6    6      695 0.021801       960 1980 1977-1989     31880

p <- ggplot(fishing, aes(x = meandepth, y = totabund/sweptarea)) +
  geom_point(alpha = 0.5) + facet_wrap(~ period) + theme_minimal() +
  labs(x = "Mean Trawl Depth (meters)",
    y = "Fish Caught Per Square Meter Trawled")
plot(p)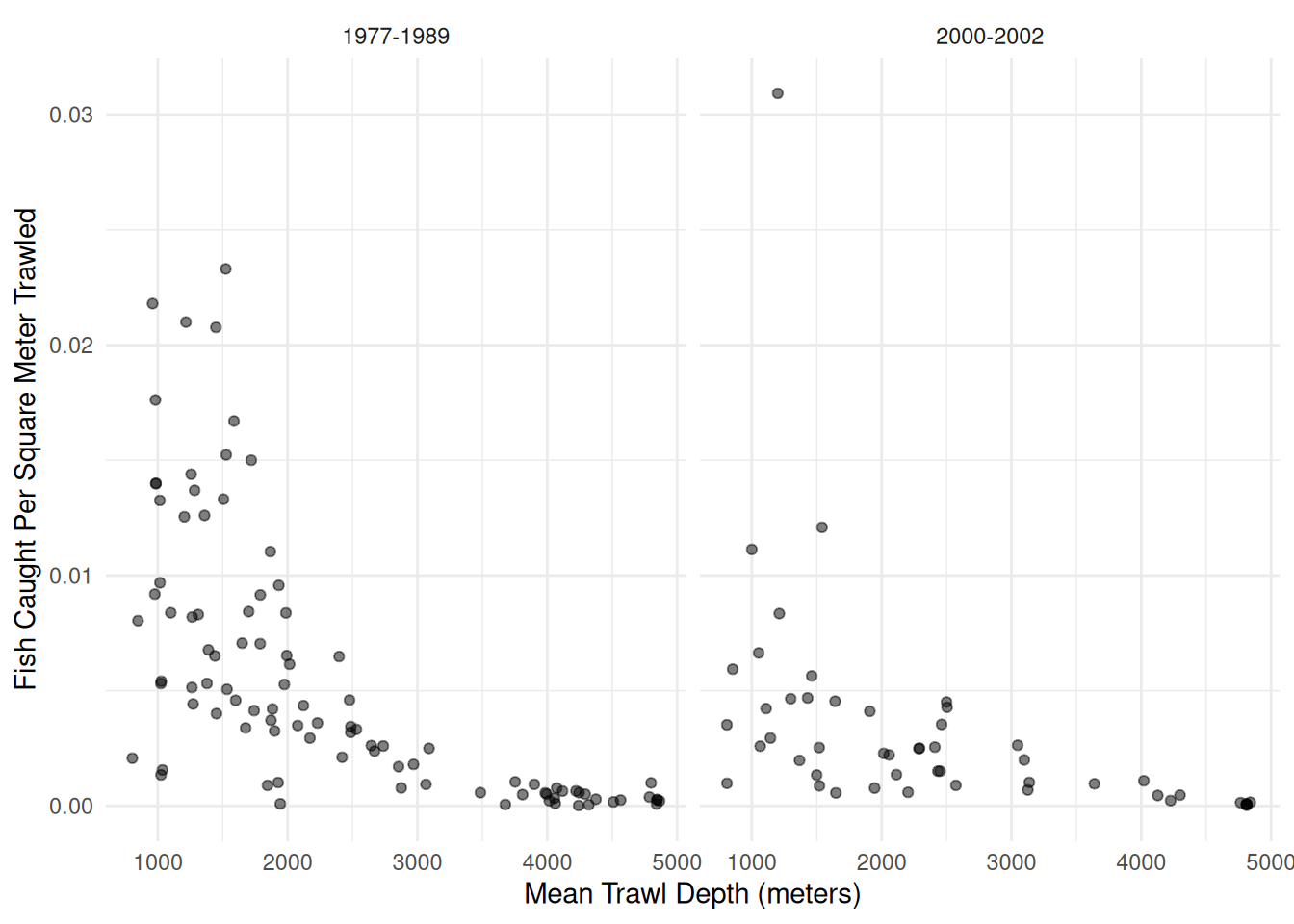

An appropriate model for these data might be as follows.

m <- glm(totabund ~ period * meandepth + offset(log(sweptarea)),
  family = poisson, data = fishing)
summary(m)$coefficients

                           Estimate Std. Error z value  Pr(>|z|)
(Intercept)               -3.422819   1.49e-02 -229.67  0.00e+00
period2000-2002           -0.771117   2.97e-02  -25.94 2.55e-148
meandepth                 -0.000971   7.96e-06 -121.94  0.00e+00
period2000-2002:meandepth  0.000132   1.52e-05    8.65  5.09e-18

d <- expand.grid(sweptarea = 1, period = c("1977-1989","2000-2002"), 
  meandepth = seq(800, 5000, length = 100))
d$yhat <- predict(m, newdata = d, type = "response")

p <- p + geom_line(aes(y = yhat), data = d)
plot(p)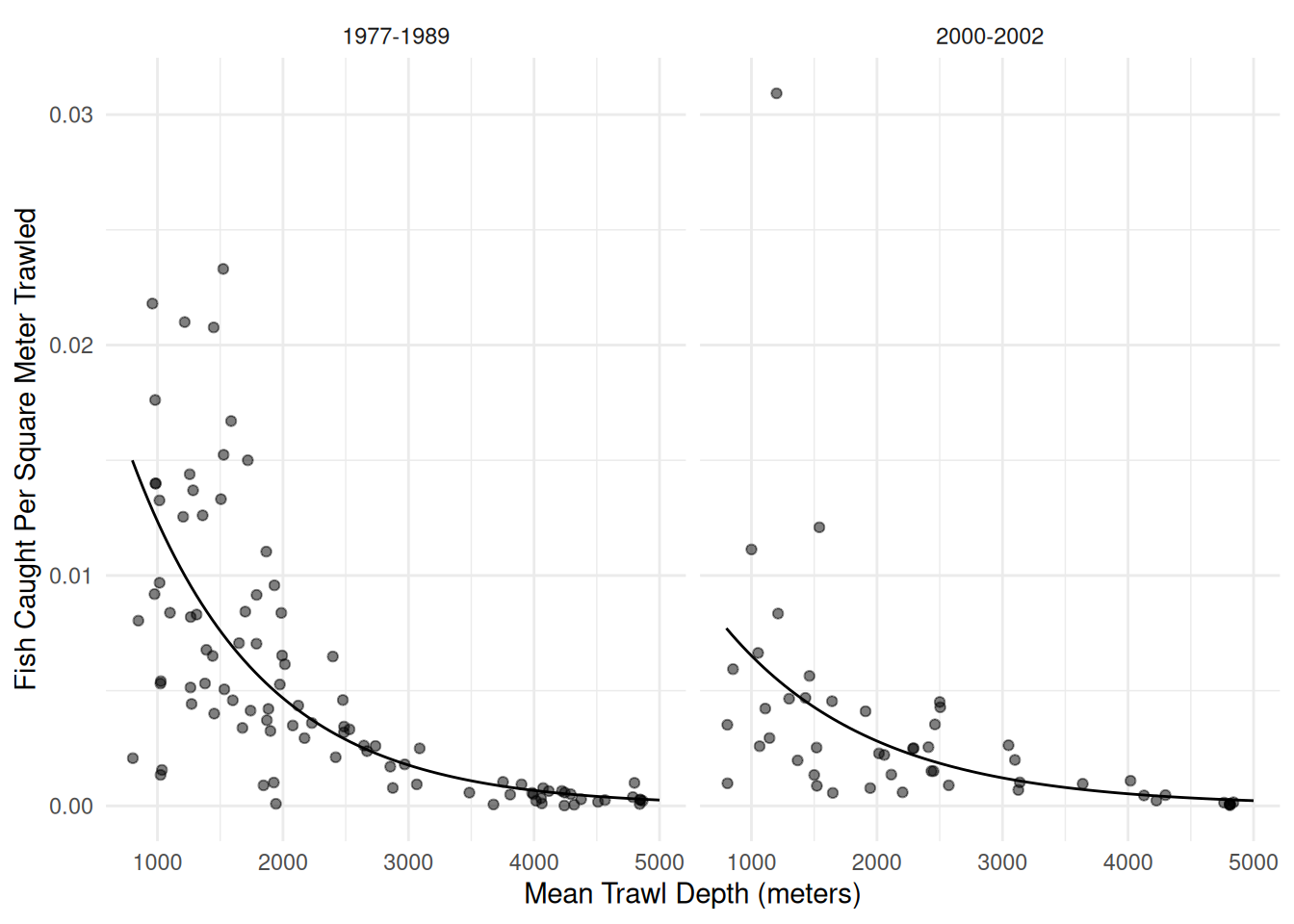

What is the expected number of fish per square meter in 1977-1989 at depths of 1000, 2000, 3000, 4000, and 5000 meters? What is it in 2000-2002?

trtools::contrast(m, 
  a = list(sweptarea = 1, 
    meandepth = c(1000,2000,3000,4000,5000), period = "1977-1989"),
  cnames = c("1000m","2000m","3000m","4000m","5000m"), tf = exp)

      estimate    lower    upper
1000m 0.012350 0.012147 0.012556
2000m 0.004676 0.004613 0.004739
3000m 0.001770 0.001728 0.001813
4000m 0.000670 0.000645 0.000696
5000m 0.000254 0.000241 0.000268

trtools::contrast(m, 
  a = list(sweptarea = 1,
    meandepth = c(1000,2000,3000,4000,5000), period = "2000-2002"),
  cnames = c("1000m","2000m","3000m","4000m","5000m"), tf = exp)

      estimate    lower    upper
1000m 0.006517 0.006325 0.006714
2000m 0.002815 0.002751 0.002881
3000m 0.001216 0.001170 0.001263
4000m 0.000525 0.000494 0.000558
5000m 0.000227 0.000208 0.000247

Here is how we can do that with emmeans.

library(emmeans)
emmeans(m, ~meandepth|period, at = list(meandepth = seq(1000, 5000, by = 1000)),
  type = "response", offset = log(1))

period = 1977-1989:
 meandepth    rate       SE  df asymp.LCL asymp.UCL
      1000 0.01235 1.04e-04 Inf   0.01215   0.01256
      2000 0.00468 3.23e-05 Inf   0.00461   0.00474
      3000 0.00177 2.17e-05 Inf   0.00173   0.00181
      4000 0.00067 1.31e-05 Inf   0.00065   0.00070
      5000 0.00025 6.90e-06 Inf   0.00024   0.00027

period = 2000-2002:
 meandepth    rate       SE  df asymp.LCL asymp.UCL
      1000 0.00652 9.91e-05 Inf   0.00633   0.00671
      2000 0.00281 3.31e-05 Inf   0.00275   0.00288
      3000 0.00122 2.38e-05 Inf   0.00117   0.00126
      4000 0.00053 1.63e-05 Inf   0.00049   0.00056
      5000 0.00023 9.80e-06 Inf   0.00021   0.00025

Confidence level used: 0.95 
Intervals are back-transformed from the log scale

Note that we can change the units of swept area very easily here. There are 10,000 square meters in a hectare. Here are the expected number of fish per hectare.

trtools::contrast(m, 
  a = list(sweptarea = 10000,
    meandepth = c(1000,2000,3000,4000,5000), period = "1977-1989"),
  cnames = c("1000m","2000m","3000m","4000m","5000m"), tf = exp)

      estimate  lower  upper
1000m   123.50 121.47 125.56
2000m    46.76  46.13  47.39
3000m    17.70  17.28  18.13
4000m     6.70   6.45   6.96
5000m     2.54   2.41   2.68

trtools::contrast(m, 
  a = list(sweptarea = 10000,
    meandepth = c(1000,2000,3000,4000,5000), period = "2000-2002"),
  cnames = c("1000m","2000m","3000m","4000m","5000m"), tf = exp)

      estimate lower upper
1000m    65.17 63.25 67.14
2000m    28.15 27.51 28.81
3000m    12.16 11.70 12.63
4000m     5.25  4.94  5.58
5000m     2.27  2.08  2.47

emmeans(m, ~meandepth|period, at = list(meandepth = seq(1000, 5000, by = 1000)),
  type = "response", offset = log(10000))

period = 1977-1989:
 meandepth  rate    SE  df asymp.LCL asymp.UCL
      1000 123.5 1.040 Inf     121.5     125.6
      2000  46.8 0.323 Inf      46.1      47.4
      3000  17.7 0.217 Inf      17.3      18.1
      4000   6.7 0.131 Inf       6.5       7.0
      5000   2.5 0.069 Inf       2.4       2.7

period = 2000-2002:
 meandepth  rate    SE  df asymp.LCL asymp.UCL
      1000  65.2 0.991 Inf      63.3      67.1
      2000  28.1 0.331 Inf      27.5      28.8
      3000  12.2 0.238 Inf      11.7      12.6
      4000   5.3 0.163 Inf       4.9       5.6
      5000   2.3 0.098 Inf       2.1       2.5

Confidence level used: 0.95 
Intervals are back-transformed from the log scale

What is the rate ratio of fish per square meter in 2000-2002 versus 1977-1989 at 1000, 2000, 3000, 4000, and 5000 meters?

trtools::contrast(m, 
  a = list(sweptarea = 1, meandepth = c(1000,2000,3000,4000,5000), period = "2000-2002"),
  b = list(sweptarea = 1, meandepth = c(1000,2000,3000,4000,5000), period = "1977-1989"),
  cnames = c("1000m","2000m","3000m","4000m","5000m"), tf = exp)

      estimate lower upper
1000m    0.528 0.510 0.546
2000m    0.602 0.586 0.618
3000m    0.687 0.656 0.719
4000m    0.784 0.729 0.842
5000m    0.894 0.809 0.989

Here it is for 1977-1989 versus 2000-2002.

trtools::contrast(m, 
  a = list(sweptarea = 1, meandepth = c(1000,2000,3000,4000,5000), period = "1977-1989"),
  b = list(sweptarea = 1, meandepth = c(1000,2000,3000,4000,5000), period = "2000-2002"),
  cnames = c("1000m","2000m","3000m","4000m","5000m"), tf = exp)

      estimate lower upper
1000m     1.90  1.83  1.96
2000m     1.66  1.62  1.71
3000m     1.46  1.39  1.52
4000m     1.28  1.19  1.37
5000m     1.12  1.01  1.24

Now using emmeans.

pairs(emmeans(m, ~meandepth*period, at = list(meandepth = seq(1000, 5000, by = 1000)),
  type = "response", offset = log(1)), by = "meandepth", infer = TRUE)

meandepth = 1000:
 contrast                  ratio     SE  df asymp.LCL asymp.UCL null z.ratio p.value
 (1977-1989) / (2000-2002)  1.90 0.0330 Inf      1.83      1.96    1  36.700  <.0001

meandepth = 2000:
 contrast                  ratio     SE  df asymp.LCL asymp.UCL null z.ratio p.value
 (1977-1989) / (2000-2002)  1.66 0.0227 Inf      1.62      1.71    1  37.200  <.0001

meandepth = 3000:
 contrast                  ratio     SE  df asymp.LCL asymp.UCL null z.ratio p.value
 (1977-1989) / (2000-2002)  1.46 0.0336 Inf      1.39      1.52    1  16.300  <.0001

meandepth = 4000:
 contrast                  ratio     SE  df asymp.LCL asymp.UCL null z.ratio p.value
 (1977-1989) / (2000-2002)  1.28 0.0468 Inf      1.19      1.37    1   6.600  <.0001

meandepth = 5000:
 contrast                  ratio     SE  df asymp.LCL asymp.UCL null z.ratio p.value
 (1977-1989) / (2000-2002)  1.12 0.0573 Inf      1.01      1.24    1   2.200  0.0288

Confidence level used: 0.95 
Intervals are back-transformed from the log scale 
Tests are performed on the log scale

How does the expected number of fish per square meter change per 1000m of depth?

# increasing depth by 1000m
trtools::contrast(m,
  a = list(sweptarea = 1, meandepth = 2000, period = c("1977-1989","2000-2002")),
  b = list(sweptarea = 1, meandepth = 1000, period = c("1977-1989","2000-2002")),
  cnames = c("1977-1989","2000-2002"), tf = exp)

          estimate lower upper
1977-1989    0.379 0.373 0.385
2000-2002    0.432 0.421 0.443

# decreasing depth by 1000m
trtools::contrast(m,
  a = list(sweptarea = 1, meandepth = 1000, period = c("1977-1989","2000-2002")),
  b = list(sweptarea = 1, meandepth = 2000, period = c("1977-1989","2000-2002")),
  cnames = c("1977-1989","2000-2002"), tf = exp)

          estimate lower upper
1977-1989     2.64  2.60  2.68
2000-2002     2.32  2.26  2.37

Here is how to do the latter with emmeans.

pairs(emmeans(m, ~meandepth*period, at = list(meandepth = c(1000,2000)),
  offset = log(1), type = "response"), by = "period", infer = TRUE)

period = 1977-1989:
 contrast                      ratio     SE  df asymp.LCL asymp.UCL null z.ratio p.value
 meandepth1000 / meandepth2000  2.64 0.0210 Inf      2.60      2.68    1 121.900  <.0001

period = 2000-2002:
 contrast                      ratio     SE  df asymp.LCL asymp.UCL null z.ratio p.value
 meandepth1000 / meandepth2000  2.31 0.0301 Inf      2.26      2.38    1  64.600  <.0001

Confidence level used: 0.95 
Intervals are back-transformed from the log scale 
Tests are performed on the log scale

Standardized Mortality Ratios

In epidemiology, the standardized mortality ratio (SMR) is the ratio of the observed number of deaths and the (estimated) expected number of deaths. Poisson regression with an offset can be used to model the SMR to determine if the number of deaths tends to be higher or lower than we would expect.

Example: Here is an example of an observational study using a Poisson regression model to investigate the relationship between lung cancer and radon exposure in counties in Minnesota.

Note: The data manipulation and plotting is quite a bit more complicated than what you will normally see in this class, but I have included it in case you might be interested to see the code.

First we will process the data containing the observed and expected number of deaths due to lung cancer, where the latter are based on the known distribution of age and gender in the county.

lung <- read.table("http://faculty.washington.edu/jonno/book/MNlung.txt", 
  header = TRUE, sep = "\t") %>% 
  mutate(obs = obs.M + obs.F, exp = exp.M + exp.F) %>% 
  dplyr::select(X, County, obs, exp) %>%
  rename(county = County) %>% 
  mutate(county = tolower(county)) %>% 
  mutate(county = ifelse(county == "red", "red lake", county))
head(lung)

  X    county obs   exp
1 1    aitkin  92  76.9
2 2     anoka 677 600.5
3 3    becker 105 107.9
4 4  beltrami 101 105.7
5 5    benton  61  81.4
6 6 big stone  32  27.4

Now we will read in data to estimate the average radon exposure of residents of each county.

radon <- read.table("http://faculty.washington.edu/jonno/book/MNradon.txt",
  header = TRUE) %>% group_by(county) %>% 
  summarize(radon = mean(radon)) %>% rename(X = county)
head(radon)

# A tibble: 6 × 2
      X radon
  <int> <dbl>
1     1  2.08
2     2  3.21
3     3  3.18
4     4  3.66
5     5  3.78
6     6  4.93

Next we merge the two data frames.

radon <- left_join(lung, radon) %>% dplyr::select(-X)
head(radon)

     county obs   exp radon
1    aitkin  92  76.9  2.08
2     anoka 677 600.5  3.21
3    becker 105 107.9  3.17
4  beltrami 101 105.7  3.66
5    benton  61  81.4  3.77
6 big stone  32  27.4  4.93

For fun we can make some plots of the data by county.

library(maps)
dstate <- map_data("state") %>% 
  filter(region == "minnesota")
dcounty <- map_data("county") %>% 
  filter(region == "minnesota") %>% 
  rename(county = subregion)
dcounty <- left_join(dcounty, radon) %>% 
  mutate(smr = obs/exp)

no_axes <- theme_minimal() + theme(
  axis.text = element_blank(),
  axis.line = element_blank(),
  axis.ticks = element_blank(),
  panel.border = element_blank(),
  panel.grid = element_blank(),
  axis.title = element_blank()
)

p <- ggplot(dcounty, aes(x = long, y = lat, group = group)) + coord_fixed(1.3) +
  geom_polygon(aes(fill = exp), color = "black", linewidth = 0.25) + 
  scale_fill_gradient(low = grey(0.95), high = grey(0.25), 
    trans = "log10", na.value = "pink") + 
  theme(legend.position = "inside", legend.position.inside = c(0.8,0.4)) + 
  no_axes + ggtitle("Expected Number of Cases") + labs(fill = "Cases")

plot(p)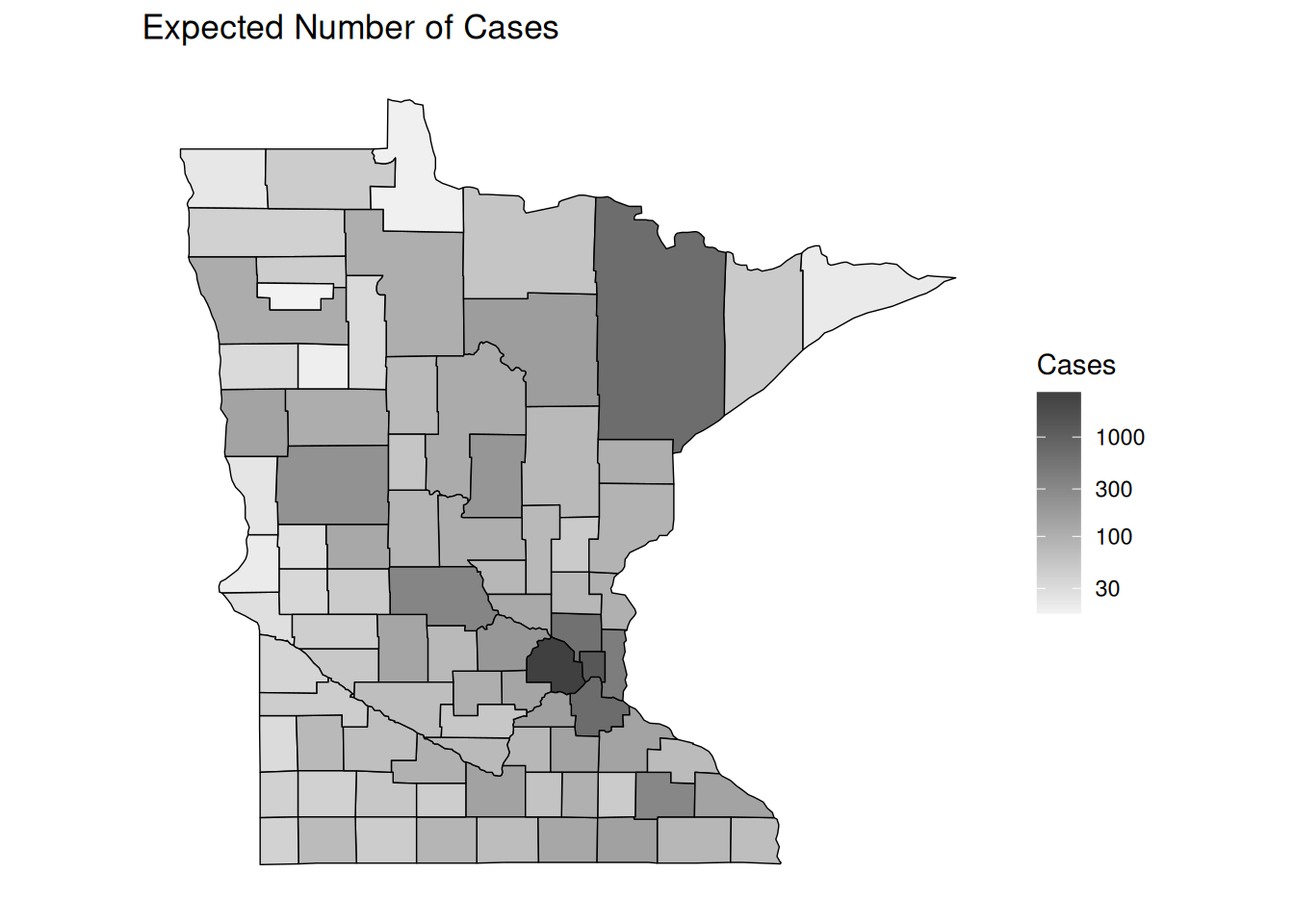

p <- ggplot(dcounty, aes(x = long, y = lat, group = group)) + coord_fixed(1.3) +
  geom_polygon(aes(fill = smr), color = "black", linewidth = 0.25) + 
  scale_fill_gradient(low = grey(0.95), high = grey(0.25), na.value = "pink") +
  theme(legend.position = "inside", legend.position.inside = c(0.8,0.4)) + 
  no_axes + ggtitle("Standardized Mortality Ratio") + labs(fill = "SMR")

plot(p)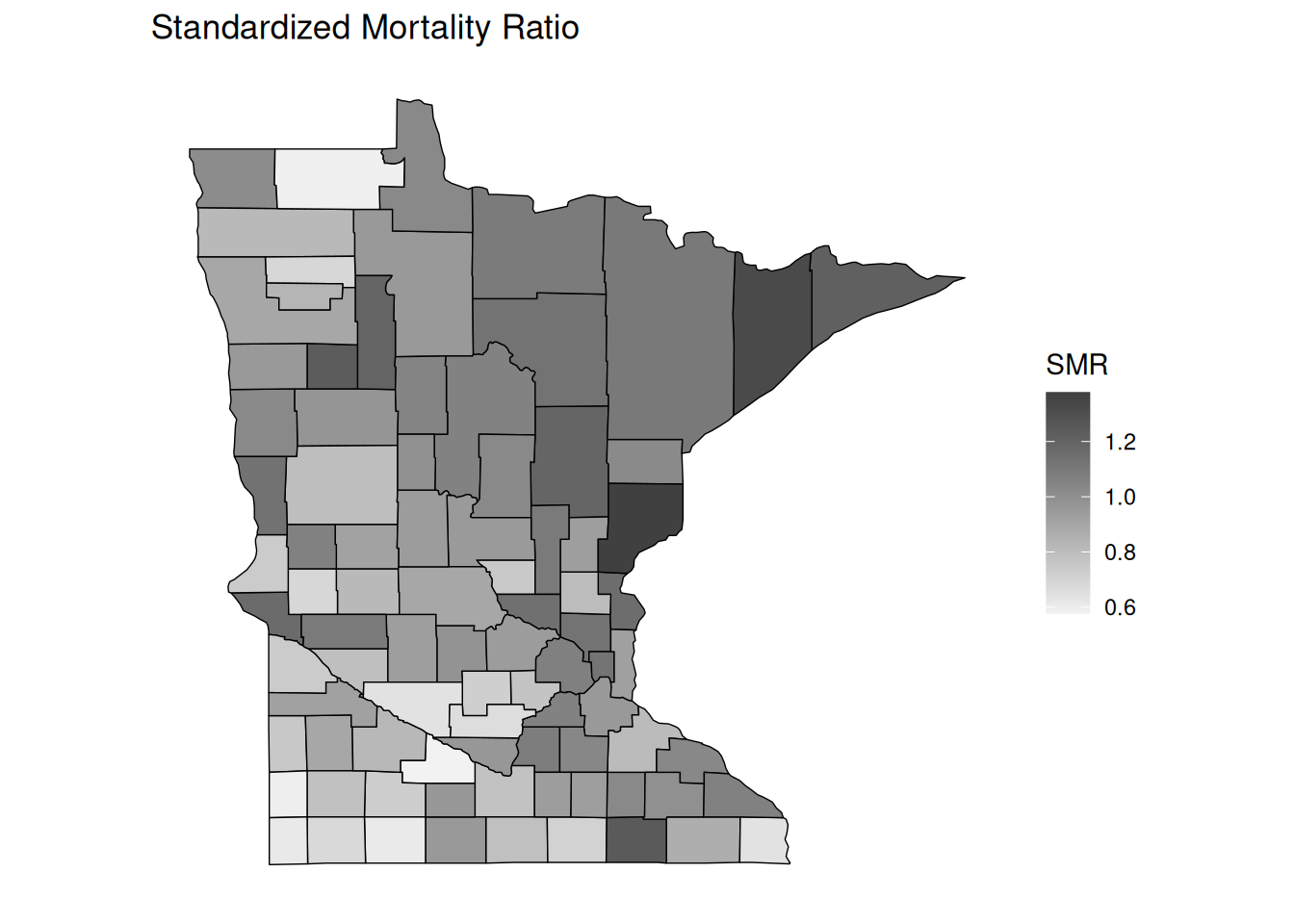

p <- ggplot(dcounty, aes(x = long, y = lat, group = group)) + coord_fixed(1.3) + 
  geom_polygon(aes(fill = radon), color = "black", linewidth = 0.25) + 
  scale_fill_gradient(low = grey(0.95), high = grey(0.25), na.value = "pink") + 
  theme(legend.position = "inside", legend.position.inside = c(0.8,0.4)) + 
  no_axes + ggtitle("Average Radon (pCi/liter)") + labs(fill = "Radon")

plot(p)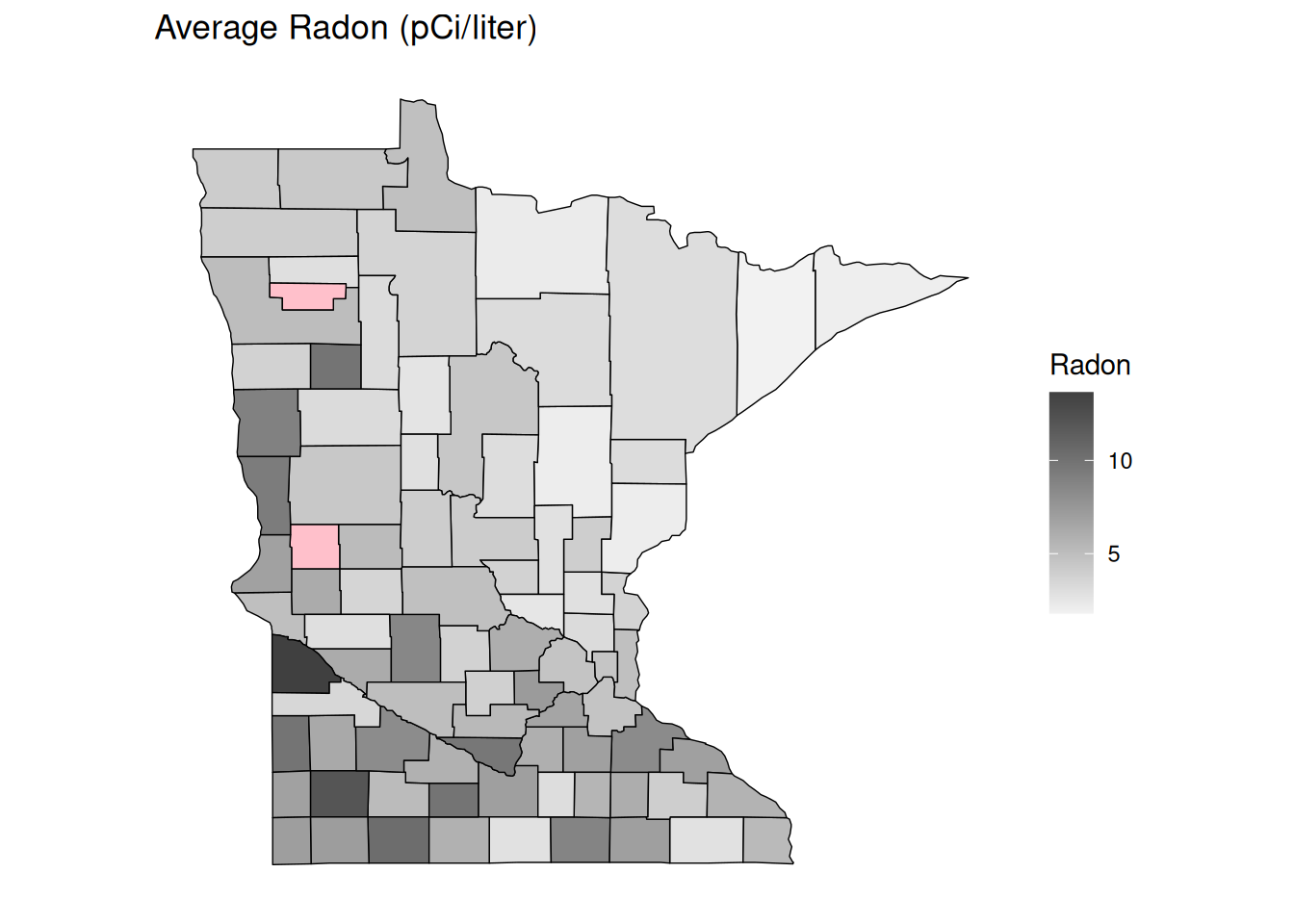

How does the expected SMR relate to radon? Consider the Poisson regression model $\log E(Y_i/E_i) = \beta_0 + \beta_1r_i,$ where $Y_i$ and $E_i$ are the observed and expected number of lung cancer deaths (or cases), respectively, in the $i$ -th county, and $r_i$ is the average radon exposure in the $i$ -th county. Here $Y_i/E_i$ is the SMR for the $i$ -th county. We can also write this model as $\log E(Y_i) = \log E_i + \beta_0 + \beta_1r_i,$ so $\log E_i$ is an offset.

m <- glm(obs ~ offset(log(exp)) + radon, family = poisson, data = dcounty)
summary(m)$coefficients

            Estimate Std. Error z value  Pr(>|z|)
(Intercept)   0.2107    0.00562    37.5 6.95e-308
radon        -0.0421    0.00119   -35.2 4.37e-272

exp(cbind(coef(m), confint(m)))

                  2.5 % 97.5 %
(Intercept) 1.235 1.221  1.248
radon       0.959 0.957  0.961

We should be careful and remember the ecological fallacy which states that relationships at the group level (e.g., county) do not necessarily hold at the individual level. Radon may be related to other variables (e.g., smoking) that affect the risk of lung cancer.