You can also download a PDF copy of this lecture.

In a discrete survival time model we model the hazard function \[ h(t) = P(T = t|T \ge t) \] (i.e., the probability of a unit not “surviving” to time \(t+1\) given that it survived to time \(t\)). This is closely related to a family of models for ordered categorical response variables that are conceptualized as a series of “stages” or “phases” of some sort. But here instead we usually model \[ P(T > t|T \ge t) \] (i.e., the probability that a unit will transition to stage \(t+1\) given that it made it to stage \(t\)). In terms of the hazard function \[ P(T > t|T \ge t) = 1 - P(T = t|T \ge t) = 1 - h(t). \] Warning: The VGAM package includes a function called margeff which computes instantaneous marginal effects for model objects created using the vglm function. To avoid conflicts, use trtools::margeff when using the margeff function from the trtools package if the VGAM package is loaded.

Example: The data frame pneumo from the package VGAM contains aggregated data of pneumoconiosis in coal miners.

library(VGAM)
print(pneumo)
  exposure.time normal mild severe
1           5.8     98    0      0
2          15.0     51    2      1
3          21.5     34    6      3
4          27.5     35    5      8
5          33.5     32   10      9
6          39.5     23    7      8
7          46.0     12    6     10
8          51.5      4    2      5

This kind of model can also be estimated using the vglm function from the VGAM package. With the original aggregated data we would specify the model as follows. Note that the order of the arguments to cbind is important. We want to order them from lowest/first to highest/last.

m <- vglm(cbind(normal,mild,severe) ~ exposure.time, 
    family = cratio(link = "logitlink"), data = pneumo)
summary(m)

Call:
vglm(formula = cbind(normal, mild, severe) ~ exposure.time, family = cratio(link = "logitlink"), 
    data = pneumo)

Coefficients: 
                Estimate Std. Error z value Pr(>|z|)    
(Intercept):1    -3.9664     0.4189   -9.47  < 2e-16 ***
(Intercept):2    -1.1133     0.7664   -1.45    0.146    
exposure.time:1   0.0963     0.0124    7.79  6.9e-15 ***
exposure.time:2   0.0355     0.0206    1.72    0.085 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Names of linear predictors: logitlink(P[Y>1|Y>=1]), logitlink(P[Y>2|Y>=2])

Residual deviance: 13.3 on 12 degrees of freedom

Log-likelihood: -29.2 on 12 degrees of freedom

Number of Fisher scoring iterations: 6 

Warning: Hauck-Donner effect detected in the following estimate(s):
'(Intercept):1'


Exponentiated coefficients:
exposure.time:1 exposure.time:2 
           1.10            1.04 
exp(cbind(coef(m), confint(m)))
                         2.5 % 97.5 %
(Intercept):1   0.0189 0.00833 0.0431
(Intercept):2   0.3285 0.07314 1.4751
exposure.time:1 1.1011 1.07469 1.1281
exposure.time:2 1.0361 0.99517 1.0787

If the data are not aggregated (i.e., one observational unit per row) then the syntax is different. Here I disaggregate the data for demonstration.

library(tidyr)
pneumosingle <- pneumo %>% pivot_longer(c(normal,mild,severe), 
  names_to = "condition", values_to = "frequency") %>% uncount(frequency)
head(pneumosingle)
# A tibble: 6 × 2
  exposure.time condition
          <dbl> <chr>    
1           5.8 normal   
2           5.8 normal   
3           5.8 normal   
4           5.8 normal   
5           5.8 normal   
6           5.8 normal   
tail(pneumosingle)
# A tibble: 6 × 2
  exposure.time condition
          <dbl> <chr>    
1          51.5 mild     
2          51.5 severe   
3          51.5 severe   
4          51.5 severe   
5          51.5 severe   
6          51.5 severe

An important step here is that we need to order the levels of condition appropriately since we cannot order it in cbind now.

pneumosingle$conditionf <- factor(pneumosingle$condition,
    levels = c("normal","mild","severe"), ordered = TRUE)
levels(pneumosingle$conditionf) # correct order
[1] "normal" "mild"   "severe"

We actually don’t need the ordered = TRUE here, as the levels argument will imply the order, but it avoids vglm throwing a warning.

Now we can specify the model as follows.

m <- vglm(conditionf ~ exposure.time, 
  family = cratio(link = "logitlink"), data = pneumosingle)
summary(m)

Call:
vglm(formula = conditionf ~ exposure.time, family = cratio(link = "logitlink"), 
    data = pneumosingle)

Coefficients: 
                Estimate Std. Error z value Pr(>|z|)    
(Intercept):1    -3.9664     0.4189   -9.47  < 2e-16 ***
(Intercept):2    -1.1133     0.7664   -1.45    0.146    
exposure.time:1   0.0963     0.0124    7.79  6.9e-15 ***
exposure.time:2   0.0355     0.0206    1.72    0.085 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Names of linear predictors: logitlink(P[Y>1|Y>=1]), logitlink(P[Y>2|Y>=2])

Residual deviance: 417 on 738 degrees of freedom

Log-likelihood: -208 on 738 degrees of freedom

Number of Fisher scoring iterations: 8 

Warning: Hauck-Donner effect detected in the following estimate(s):
'(Intercept):1'


Exponentiated coefficients:
exposure.time:1 exposure.time:2 
           1.10            1.04 
exp(cbind(coef(m), confint(m)))
                         2.5 % 97.5 %
(Intercept):1   0.0189 0.00833 0.0431
(Intercept):2   0.3285 0.07314 1.4751
exposure.time:1 1.1011 1.07469 1.1281
exposure.time:2 1.0361 0.99517 1.0787

Now suppose we want to plot the model. First we can compute the probability of each condition as a function of exposure.

d <- data.frame(exposure.time = seq(5, 55, length = 100))
d <- cbind(d, predict(m, newdata = d, type = "response"))
head(d)
  exposure.time normal   mild  severe
1          5.00  0.970 0.0214 0.00838
2          5.51  0.969 0.0223 0.00890
3          6.01  0.967 0.0232 0.00945
4          6.52  0.966 0.0242 0.01003
5          7.02  0.964 0.0253 0.01064
6          7.53  0.962 0.0263 0.01129

We can use the pivot_longer function from the tidyr package to reshape the data for plotting.

library(tidyr)
d <- d %>% pivot_longer(c(normal,mild,severe), 
  names_to = "condition", values_to = "probability")
head(d)
# A tibble: 6 × 3
  exposure.time condition probability
          <dbl> <chr>           <dbl>
1          5    normal        0.970  
2          5    mild          0.0214 
3          5    severe        0.00838
4          5.51 normal        0.969  
5          5.51 mild          0.0223 
6          5.51 severe        0.00890
tail(d)
# A tibble: 6 × 3
  exposure.time condition probability
          <dbl> <chr>           <dbl>
1          54.5 normal          0.218
2          54.5 mild            0.239
3          54.5 severe          0.543
4          55   normal          0.209
5          55   mild            0.239
6          55   severe          0.552
p <- ggplot(d, aes(x = exposure.time, y = probability, color = condition)) + 
  geom_line() + theme_minimal() + 
  labs(x = "Exposure (Years)", y = "Probability", color = "Condition")
plot(p)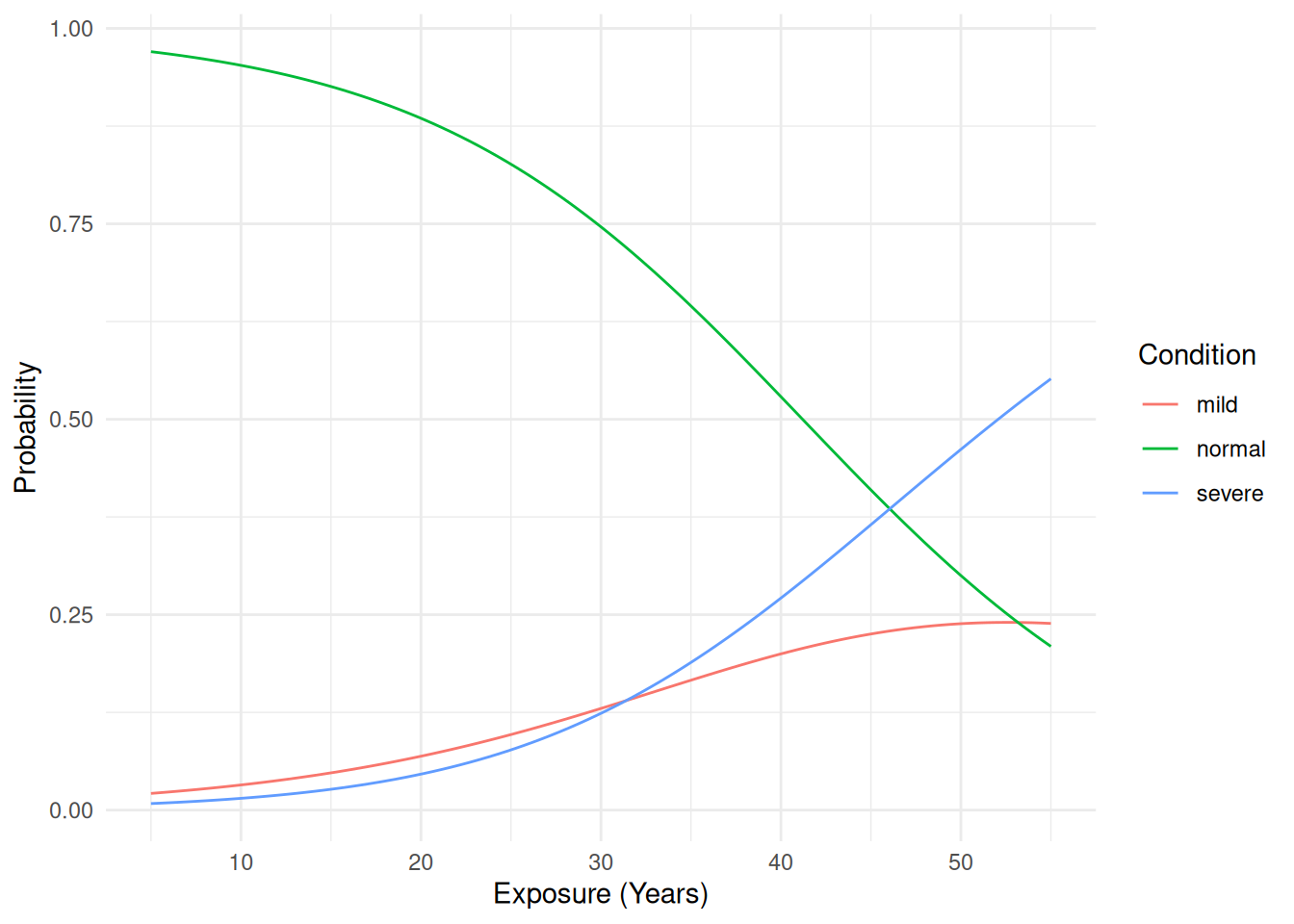

Alternatively we can plot the probability of passing from one condition to the next — i.e., \(P(Y>y|Y \ge y)\). But we need to compute those probabilities using the following fact. \[ P(Y > y|Y \ge y) = \frac{P(Y > y \text{ and } Y \ge y)}{P(Y \ge y)} = \frac{P(Y > y)}{P(Y \ge y)}. \] Note that this uses the definition of a conditional probability and the fact that if \(Y > y\) and \(Y \ge y\) then \(Y > y\). So \[ P(Y > 1|Y \ge 1) = \frac{P(Y > 1)}{P(Y \ge 1)} = \frac{P(Y=2) + P(Y=3)}{P(Y=1) + P(Y=2) + P(Y=3)}, \] and \[ P(Y > 2|Y \ge 2) = \frac{P(Y > 2)}{P(Y \ge 2)} = \frac{P(Y=3)}{P(Y=2) + P(Y=3)}. \] So we can compute the probability by adding together category probabilities.

d <- data.frame(exposure.time = seq(5, 55, length = 100))
d <- cbind(d, predict(m, newdata = d, type = "response"))
# probability of going from normal to mild -- i.e., P(Y > normal|Y >= normal)
d$nm <- with(d, (mild + severe) / (normal + mild + severe))
# probability of going from mild to severe -- i.e., P(Y > mild|Y >= mild)
d$ms <- with(d, severe / (mild + severe))
head(d)
  exposure.time normal   mild  severe     nm    ms
1          5.00  0.970 0.0214 0.00838 0.0297 0.282
2          5.51  0.969 0.0223 0.00890 0.0312 0.285
3          6.01  0.967 0.0232 0.00945 0.0327 0.289
4          6.52  0.966 0.0242 0.01003 0.0343 0.293
5          7.02  0.964 0.0253 0.01064 0.0359 0.296
6          7.53  0.962 0.0263 0.01129 0.0376 0.300

Remove original category probabilities just for clarity, reshape the data, and plot.

d$normal <- NULL
d$mild <- NULL
d$severe <- NULL
d <- d %>% pivot_longer(c(nm,ms), names_to = "transition", values_to = "probability")
head(d)
# A tibble: 6 × 3
  exposure.time transition probability
          <dbl> <chr>            <dbl>
1          5    nm              0.0297
2          5    ms              0.282 
3          5.51 nm              0.0312
4          5.51 ms              0.285 
5          6.01 nm              0.0327
6          6.01 ms              0.289 
tail(d)
# A tibble: 6 × 3
  exposure.time transition probability
          <dbl> <chr>            <dbl>
1          54.0 nm               0.774
2          54.0 ms               0.690
3          54.5 nm               0.782
4          54.5 ms               0.694
5          55   nm               0.791
6          55   ms               0.698
p <- ggplot(d, aes(x = exposure.time, y = probability, color = transition)) + 
  geom_line() + theme_minimal() + 
  labs(x = "Exposure (Years)", y = "Probability", color = "Transition")
plot(p)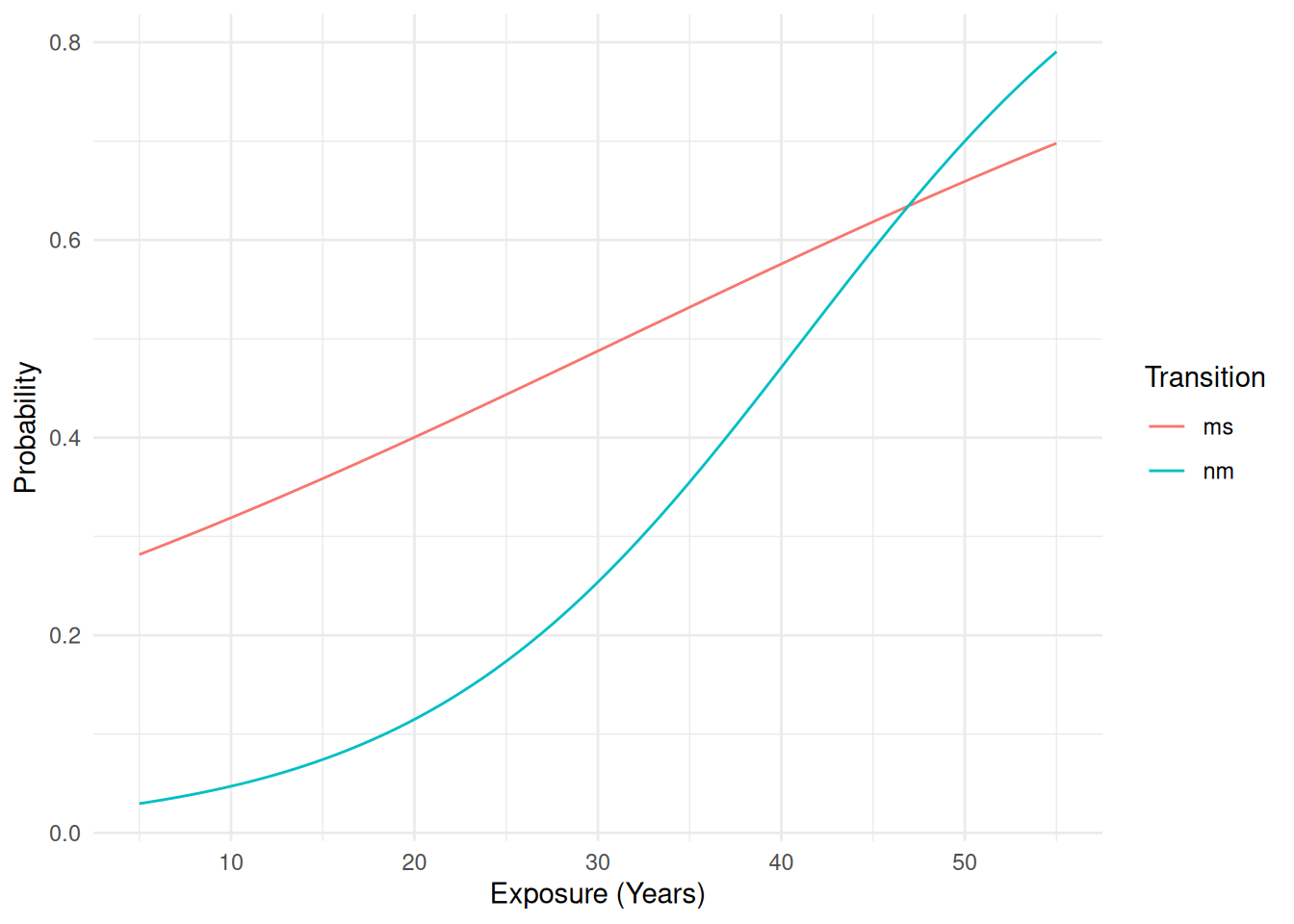

Example: Consider again the firstsex data.

firstsex <- read.table("https://stats.idre.ucla.edu/stat/examples/alda/firstsex.csv", 
  sep = ",", header = TRUE)
firstsex$parent_trans <- factor(firstsex$pt, 
  levels = c(0,1), labels = c("no","yes"))

The discrete survival model can be estimated using vglm if the right-censoring is always at the highest observed time, which it is here (grade 12). We need to create a new “grade” for those cases where sex had not occurred for the first time in grade 12 (this represents first sex after HS, if at all).

firstsex$time <- ifelse(firstsex$censor == 1, 13, firstsex$time)

Probabilities of the form \(P(Y = y|Y \ge y)\) can be modeled using vglm if we use the sratio family. Here we do not need to worry about the ordering of the response variable because it is implied by the ordering of the grade numbers.

m <- vglm(time ~ parent_trans, data = firstsex,
  family = sratio(link = "logitlink", parallel = TRUE))
summary(m)

Call:
vglm(formula = time ~ parent_trans, family = sratio(link = "logitlink", 
    parallel = TRUE), data = firstsex)

Coefficients: 
                Estimate Std. Error z value Pr(>|z|)    
(Intercept):1     -2.994      0.318   -9.43  < 2e-16 ***
(Intercept):2     -3.700      0.420   -8.81  < 2e-16 ***
(Intercept):3     -2.281      0.273   -8.36  < 2e-16 ***
(Intercept):4     -1.823      0.258   -7.06  1.7e-12 ***
(Intercept):5     -1.654      0.269   -6.15  7.8e-10 ***
(Intercept):6     -1.179      0.270   -4.36  1.3e-05 ***
parent_transyes    0.874      0.218    4.02  5.9e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Number of linear predictors:  6 

Names of linear predictors: logitlink(P[Y=1|Y>=1]), logitlink(P[Y=2|Y>=2]), 
logitlink(P[Y=3|Y>=3]), logitlink(P[Y=4|Y>=4]), logitlink(P[Y=5|Y>=5]), logitlink(P[Y=6|Y>=6])

Residual deviance: 635 on 1073 degrees of freedom

Log-likelihood: -317 on 1073 degrees of freedom

Number of Fisher scoring iterations: 5 

Warning: Hauck-Donner effect detected in the following estimate(s):
'(Intercept):2'


Exponentiated coefficients:
parent_transyes 
            2.4

Note that specifying parallel = TRUE means that the effect of pt is the same at each grade (i.e., no interaction between grade and pt). Note that the odds ratio for parenting transition (pt) is the same as what we obtained in the previous lecture.

exp(cbind(coef(m), confint(m)))
                        2.5 % 97.5 %
(Intercept):1   0.0501 0.0269 0.0933
(Intercept):2   0.0247 0.0109 0.0563
(Intercept):3   0.1022 0.0599 0.1744
(Intercept):4   0.1616 0.0974 0.2681
(Intercept):5   0.1912 0.1129 0.3240
(Intercept):6   0.3076 0.1811 0.5223
parent_transyes 2.3956 1.5641 3.6691

The other parameters are not the same because this model is parameterized differently, using indicator variables for all grades (called (Intercept) here for reasons we will see in the next lecture) and then dropping the overall intercept term.

firstsex <- read.table("https://stats.idre.ucla.edu/stat/examples/alda/firstsex.csv", 
  sep = ",", header = TRUE)
firstsex$parent_trans <- factor(firstsex$pt, 
  levels = c(0,1), labels = c("no","yes"))
firstsex$status <- ifelse(firstsex$censor == 1, 0, 1)
firstsex <- trtools::dsurvbin(firstsex, "time", "status")
m <- glm(y ~ -1 + t + parent_trans, 
  family = binomial, data = firstsex)
summary(m)$coefficients
                Estimate Std. Error z value Pr(>|z|)
t7                -2.994      0.318   -9.43 4.07e-21
t8                -3.700      0.420   -8.80 1.37e-18
t9                -2.281      0.272   -8.37 5.55e-17
t10               -1.823      0.258   -7.05 1.77e-12
t11               -1.654      0.269   -6.15 7.89e-10
t12               -1.179      0.272   -4.34 1.42e-05
parent_transyes    0.874      0.217    4.02 5.86e-05
exp(cbind(coef(m), confint(m)))
                         2.5 % 97.5 %
t7              0.0501 0.02588 0.0903
t8              0.0247 0.00991 0.0526
t9              0.1022 0.05847 0.1705
t10             0.1616 0.09543 0.2635
t11             0.1912 0.11043 0.3181
t12             0.3076 0.17740 0.5163
parent_transyes 2.3956 1.57661 3.7041

Example: We can estimate the discrete survival model for the cycles data as follows. Note that we do not need to do anything for the censoring here because all observations censored at 12 are recorded at 13 (much like we did with the firstsex data).

library(trtools)
m <- vglm(cycles ~ mother, data = cycles, 
   family = sratio(link = "logitlink", parallel = TRUE ~ 1 + mother))
summary(m)

Call:
vglm(formula = cycles ~ mother, family = sratio(link = "logitlink", 
    parallel = TRUE ~ 1 + mother), data = cycles)

Coefficients: 
                Estimate Std. Error z value Pr(>|z|)    
(Intercept)       -1.242      0.116   -10.7  < 2e-16 ***
mothernonsmoker    0.541      0.129     4.2  2.7e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Number of linear predictors:  12 

Names of linear predictors: logitlink(P[Y=1|Y>=1]), logitlink(P[Y=2|Y>=2]), 
logitlink(P[Y=3|Y>=3]), logitlink(P[Y=4|Y>=4]), logitlink(P[Y=5|Y>=5]), logitlink(P[Y=6|Y>=6]), 
logitlink(P[Y=7|Y>=7]), logitlink(P[Y=8|Y>=8]), logitlink(P[Y=9|Y>=9]), logitlink(P[Y=10|Y>=10]), 
logitlink(P[Y=11|Y>=11]), logitlink(P[Y=12|Y>=12])

Residual deviance: 2258 on 7030 degrees of freedom

Log-likelihood: -1129 on 7030 degrees of freedom

Number of Fisher scoring iterations: 5 

No Hauck-Donner effect found in any of the estimates
exp(cbind(coef(m), confint(m)))
                      2.5 % 97.5 %
(Intercept)     0.289  0.23  0.363
mothernonsmoker 1.718  1.33  2.213

Same results as in the last lecture except confidence interval is slightly different (the confidence interval here is a Wald confidence interval as opposed to a profile likelihood interval). Note that the argument parallel = TRUE ~ 1 + mother forces the parameters to be the same across categories (i.e., cycles).