Monday, Mar 6
You can also download a PDF copy of this lecture.
Statistical Significance
A statistically significant result is one that is decidedly not due to “ordinary variation” in the data (i.e., not due to chance or not a coincidence). Statistical tests (aka significance tests or statistical hypothesis tests or hypothesis tests) are how we decide whether or not an observed result is statistically significant.
Is a Coin Fair?
Suppose we flip a coin \(n\) times. We can consider the observation of each flip to be a random variable with the following distribution.| \(x\) | \(P(x)\) |
|---|---|
| Heads | \(p\) |
| Tails | \(1-p\) |
The value of \(p\) implies something about the coin.
- If \(p\) \(=\) 0.5 the coin is fair.
- If \(p\) \(\neq\) 0.5 the coin is not fair.
Assume we do not know the value of \(p\). We flip the coin 30 times to produce a sample of \(n\) = 30 observations. It comes up heads 20 times, so \(\hat{p}\) = 20/30 = 2/3 \(\approx\) 0.67. What might we decide about \(p\)?
- Conclude that \(p\) \(=\) 0.5. The result that \(\hat{p}\) \(=\) 2/3 is not statistically significant.
- Conclude that \(p\) \(\neq\) 0.5. The result that \(\hat{p}\) \(=\) 2/3 is statistically significant.
How do we decide?
Can Milena Read?
Suppose Milena plays \(n\) games of Pounce. We can consider the observation of her response to a single game to be a random variable with the following distribution.| \(x\) | \(P(x)\) |
|---|---|
| Correct | \(p\) |
| Incorrect | \(1-p\) |
The value of \(p\) implies something about Milena’s reading ability.
- Milena cannot read. She is guessing so \(p\) \(=\) 1/3.
- Milena can read (somewhat) so \(p\) \(>\) 1/3.
We do not know the value of \(p\). Milena played Pounce 50 times to produce a sample of \(n\) = 50 observations. She selected the correct word 25 times, so \(\hat{p}\) = 25/50 = 0.5. What would we decide about \(p\)?
- Conclude that \(p\) \(=\) 1/3. The result that \(\hat{p}\) \(=\) 0.5 is not statistically significant.
- Conclude that \(p\) \(>\) 1/3. The result that \(\hat{p}\) \(=\) 0.5 is statistically significant.
What do we decide?
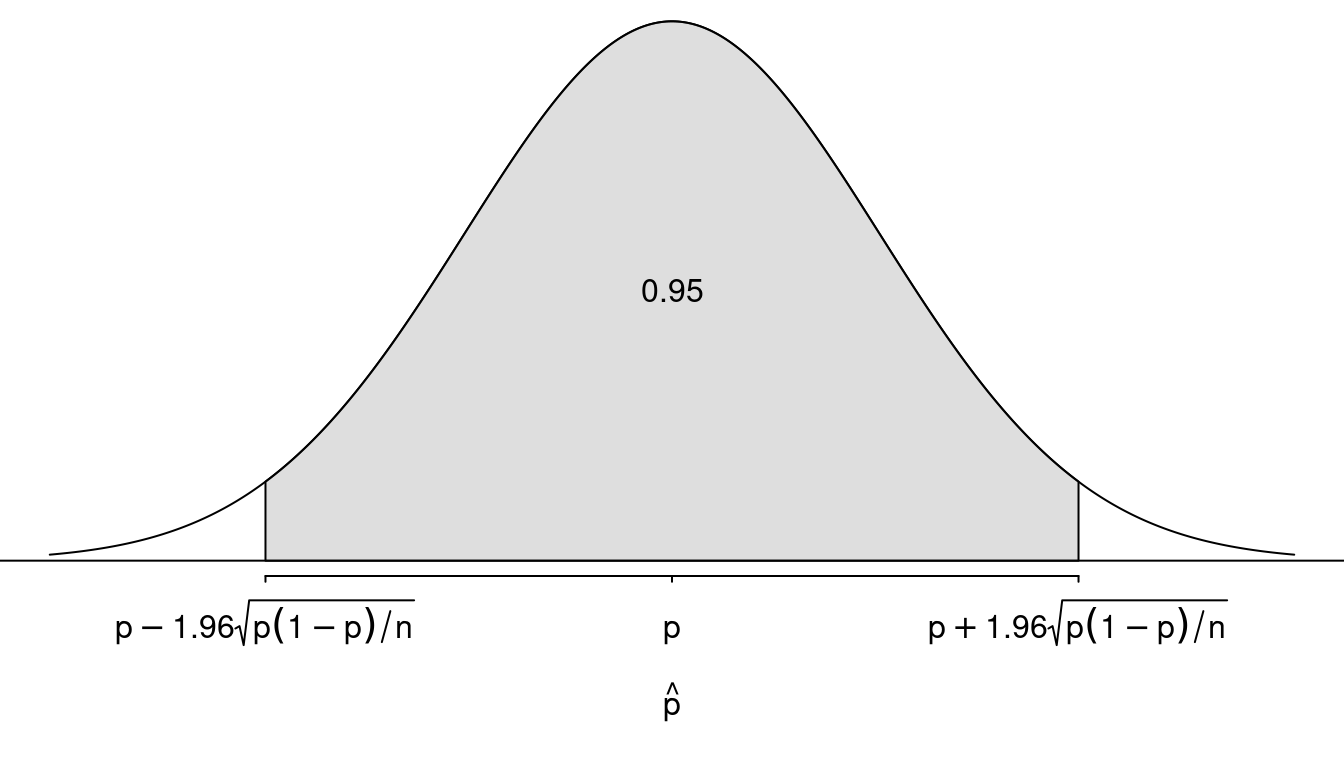
The Sampling Distribution of \(\hat{p}\)
What do we know about the sampling distribution of \(\hat{p}\)?
- The mean of \(\hat{p}\) is \(p\).
- The standard deviation (i.e., standard error) of \(\hat{p}\) is \[ \sqrt{\frac{p(1-p)}{n}}. \]
- The shape of the sampling distribution is approximately that of a normal distribution.
This is the sampling distribution of \(\hat{p}\).
 It is convenient to convert \(\hat{p}\)
into a \(z\)-score using the formula
\[
z = \frac{\hat{p}-p}{\sqrt{p(1-p)/n}}.
\]
It is convenient to convert \(\hat{p}\)
into a \(z\)-score using the formula
\[
z = \frac{\hat{p}-p}{\sqrt{p(1-p)/n}}.
\]
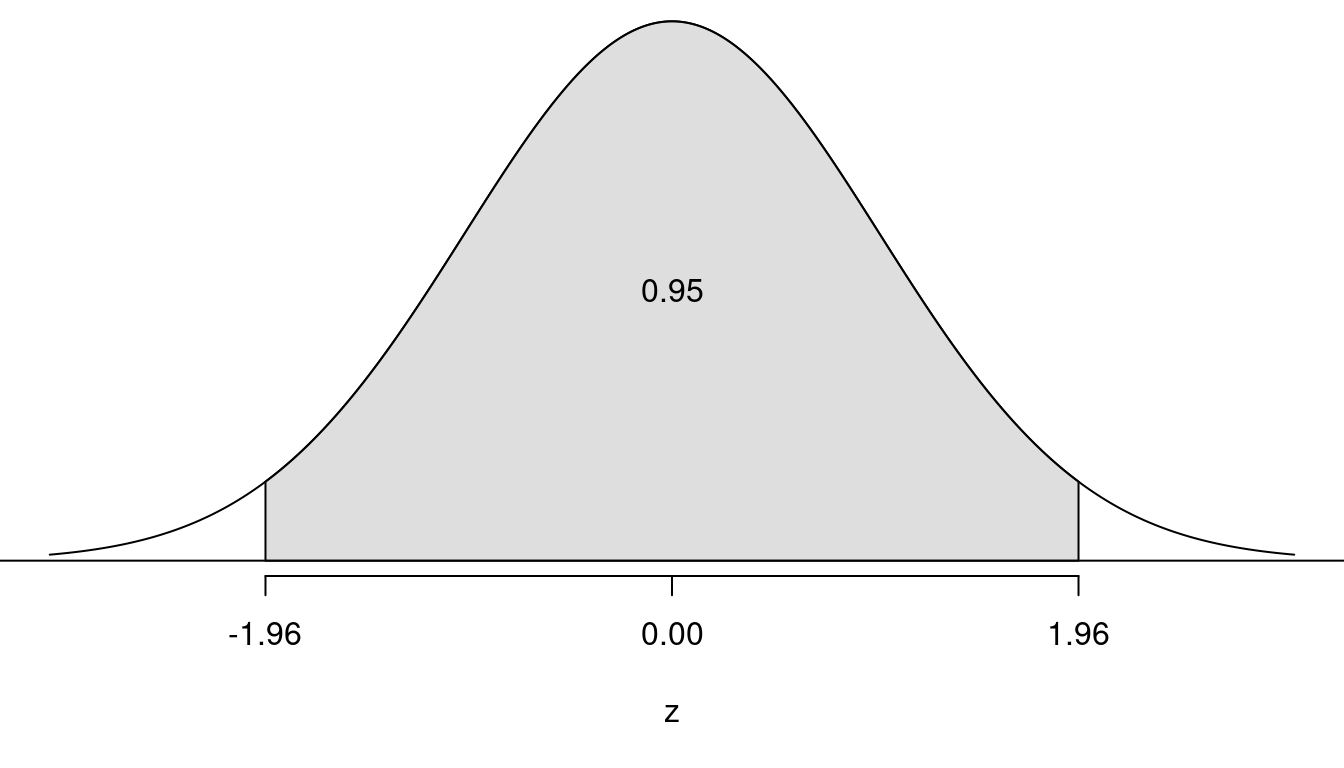
This is the sampling distribution of \(z\).
 But we do not know the value of \(p\)!
But we do not know the value of \(p\)!
Null and Alternative Hypotheses
Null Hypothesis \((H_0)\): Usually the hypothesis of “no effect” (e.g., nothing is “happening”). In practice the null hypothesis is often that the parameter equals a specific value (although we will consider the case when it may be a range of values when we discuss composite null hypotheses).
Alternative Hypothesis \((H_a)\): Usually the hypothesis of an “effect” (e.g., something is “happening”). In practice the alternative hypothesis is usually that the parameter is in a range of values.
What would the null and alternative hypotheses be for the examples above?
Test Statistics
A test statistic measures the discrepancy between the point estimate of the parameter and the hypothesized value of the parameter. A test statistic is computed under the assumption that the null hypothesis is true.
Example: The \(z\)-score \[ z = \frac{\hat{p}-p}{\sqrt{p(1-p)/n}} \] is a test statistic. What would be the value of the test statistic for the examples above?
Decision Making
Modus Tollens: If A then B. Not B. Therefore not A.
Example: If someone is a Hobbit (A), then their feet will be hairy (B). Your feet are not hairy (not B). Therefore you are not a Hobbit (not A).
Example: If it rains today (A), then the ground will be wet (B). The ground is not wet (not B). Therefore it did not rain today (not A).
“Probabilistic” Modus Tollens: If \(H_0\) is true (A), then the test statistic is likely to be a “typical” value (B). The test statistics is not a “typical” value (not B). Therefore \(H_0\) is decidedly false (not A).
Example: If \(H_0\) is true (A), then it is likely that -1.96 < \(z\) < 1.96 (B). So if \(z\) > 1.96 or \(z\) < -1.96 (not B), then we decide that \(H_0\) is not true (not A).
What can we decide?
The test statistic is a “typical” value when \(H_0\) is true. Do not reject \(H_0\). The result is not statistically significant.
The test statistic is not a “typical” value when \(H_0\) is true. Reject \(H_0\). The result is statistically significant.
Note: This is not a true modus tollens argument. This argument can lead us to the wrong conclusion because it is still possible to observe an atypical value of the test statistic even if \(H_0\) is true.
Example: What might we decide for the previous examples?
More Platies!
Do female platies have a preference for a yellow-tailed male?
 In 67 out of 84 observations, the female platy spent a majority of her
time with the yellow-tailed male. Is this statistically significant?
In 67 out of 84 observations, the female platy spent a majority of her
time with the yellow-tailed male. Is this statistically significant?