You can also download a PDF copy of this lecture.

Population and Sampling Distributions

A population distribution is the probability distribution of one observation of a random variable (i.e., \(x\)).

A sampling distribution is the probability distribution of a statistic (e.g., \(\bar{x}\) or \(\hat{p}\)) which is a function of a sample of observations of a random variable (i.e., \(x_1, x_2, \dots, x_n\)).

The sampling distribution depends on (a) the population distribution and (b) the design.

Properties of the Sampling Distribution of \(\bar{x}\)

Assume (a) that we have a population distribution of a quantitative variable \(x\) with mean \(\mu_x\) and standard deviation \(\sigma_x\), and (b) we observe a sample of \(n\) observations and compute the mean (\(\bar{x}\)) from this sample. Note that I will use a subscript on \(\mu\) and \(\sigma\) to make explicit the variable in question.

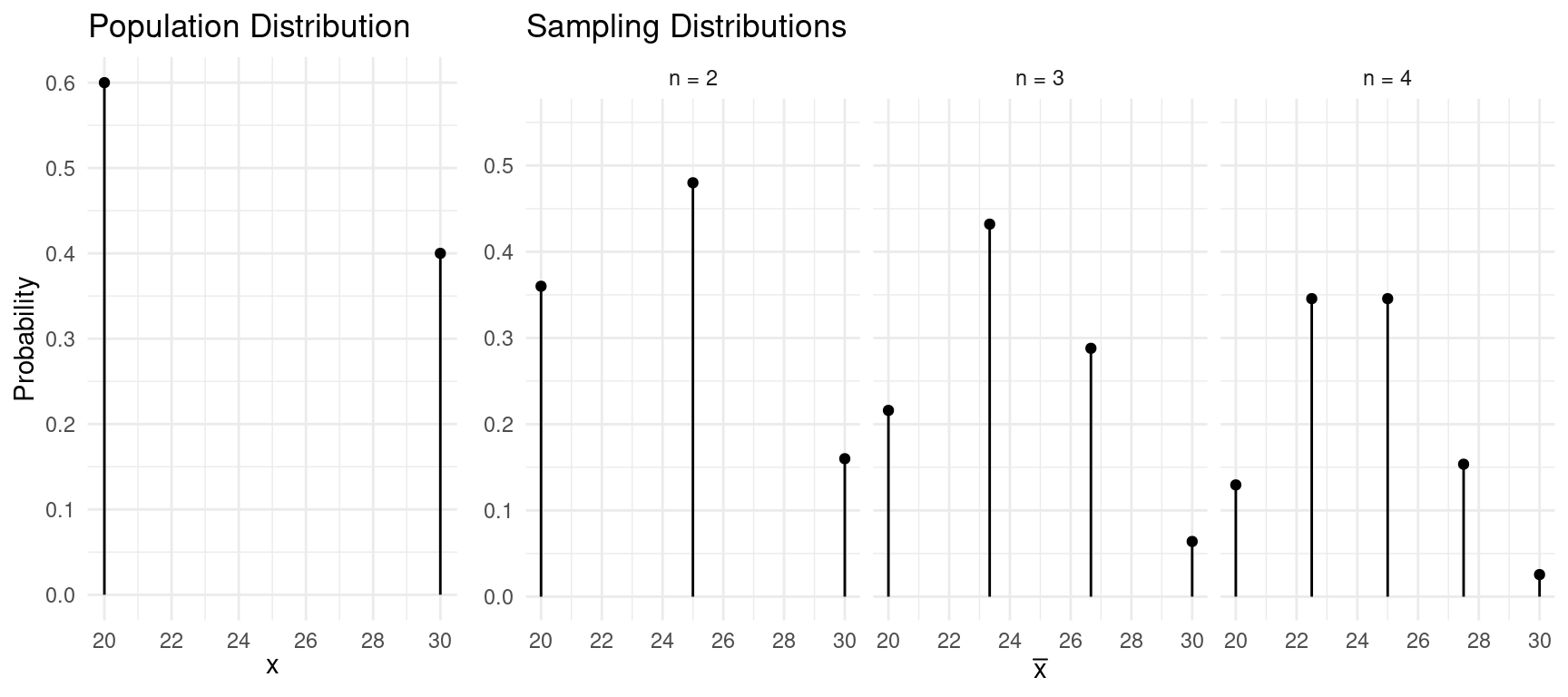
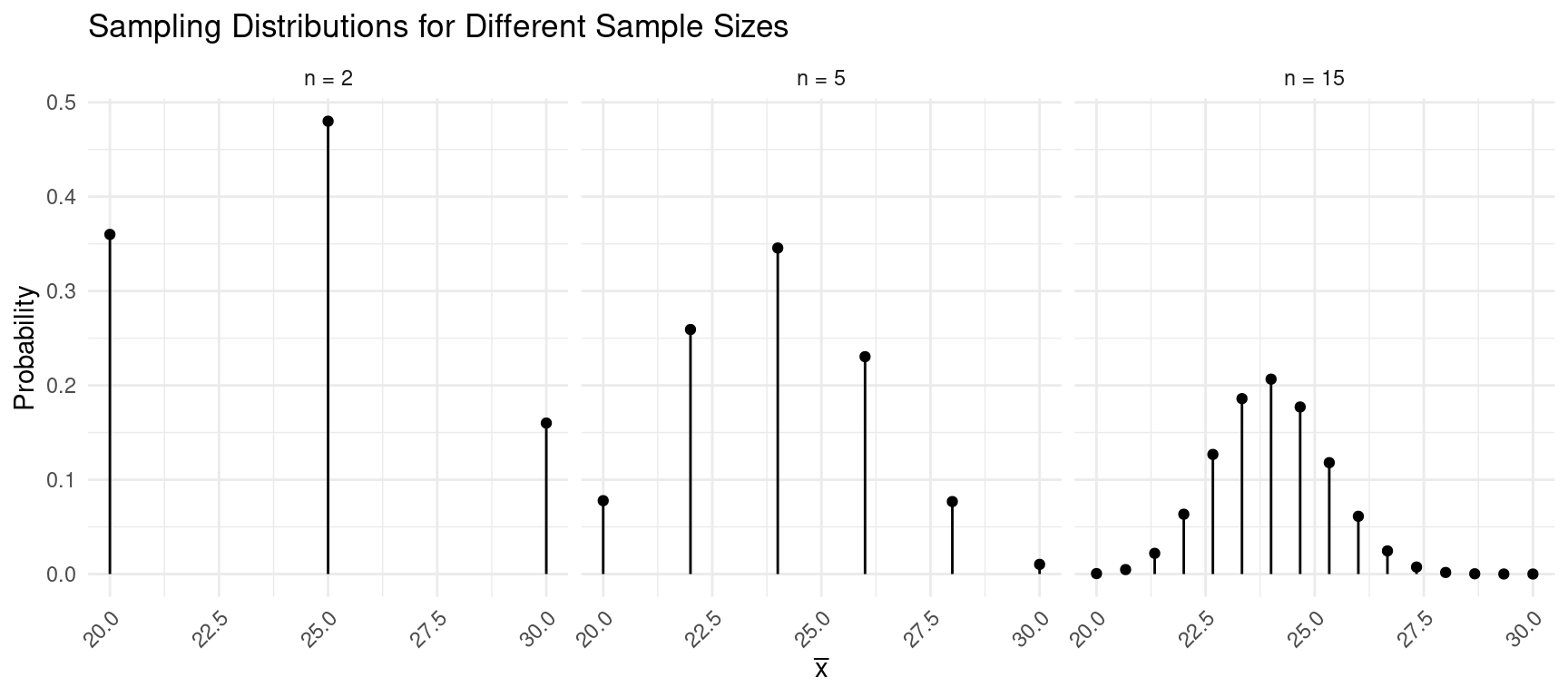
Example: Consider the following population distribution, and several sampling distributions of \(\bar{x}\) based on samples of \(n\) = 2, 3, or 4 observations.

Population Distribution
\(x\) \(P(x)\)
20 0.6
30 0.4

\[\begin{align*} \mu_{x} & = 24 \\ \sigma_{x} & \approx 4.9 \end{align*}\]

Sampling Distribution of \(\bar{x}\), \(n\) = 2
\(\bar{x}\) \(P(\bar{x})\)
20 0.36
25 0.48
30 0.16

\[\begin{align*} \mu_{\bar{x}} & = 24 \\ \sigma_{\bar{x}} & \approx 3.46 \end{align*}\]

Sampling Distribution of \(\bar{x}\), \(n\) = 3
\(\bar{x}\) \(P(\bar{x})\)
20.00 0.216
23.33 0.432
26.67 0.288
30.00 0.064

\[\begin{align*} \mu_{\bar{x}} & = 24 \\ \sigma_{\bar{x}} & \approx 2.83 \end{align*}\]

Sampling Distribution of \(\bar{x}\), \(n\) = 4
\(\bar{x}\) \(P(\bar{x})\)
20.0 0.1296
22.5 0.3456
25.0 0.3456
27.5 0.1536
30.0 0.0256

\[\begin{align*} \mu_{\bar{x}} & = 24 \\ \sigma_{\bar{x}} & \approx 2.45 \end{align*}\]

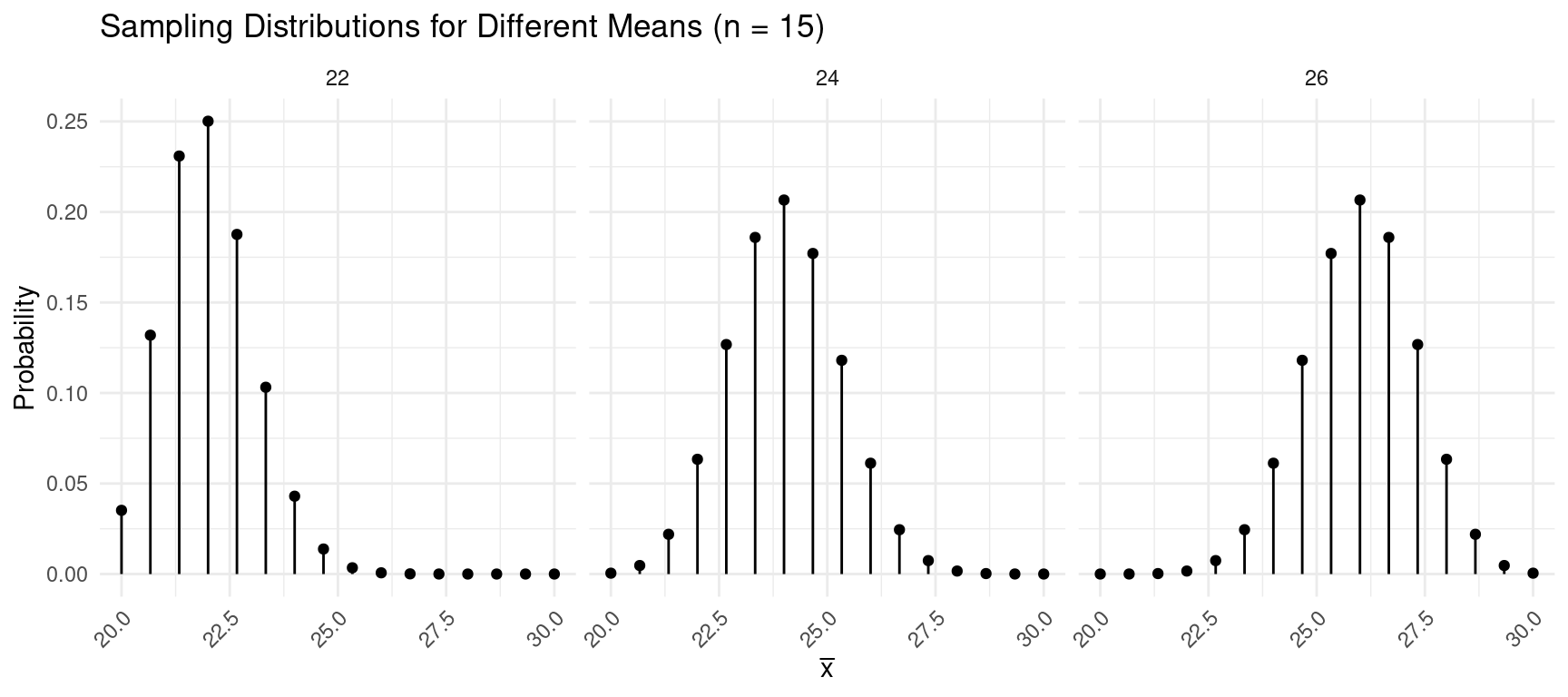
Mean and Standard Deviation of \(\bar{x}\)

Assume that \(x\) has a mean of \(\mu\) and a standard deviation of \(\sigma\), and assume a sample of \(n\) observations.

  1. The mean of the \(\bar{x}\) is \(\mu_x\) — i.e., \(\mu_{\bar{x}} = \mu_x\).
  2. The standard deviation of \(\bar{x}\) is \(\sigma_x/\sqrt{n}\) — i.e., \(\sigma_{\bar{x}} = \sigma_x/\sqrt{n}\)).

Example: Assuming that \(\mu_x\) = 24 and \(\sigma_x \approx\) 4.9, what are the mean and standard deviation of \(\bar{x}\) based on a sample of \(n\) = 16 observations? What about \(n\) = 25 observations?

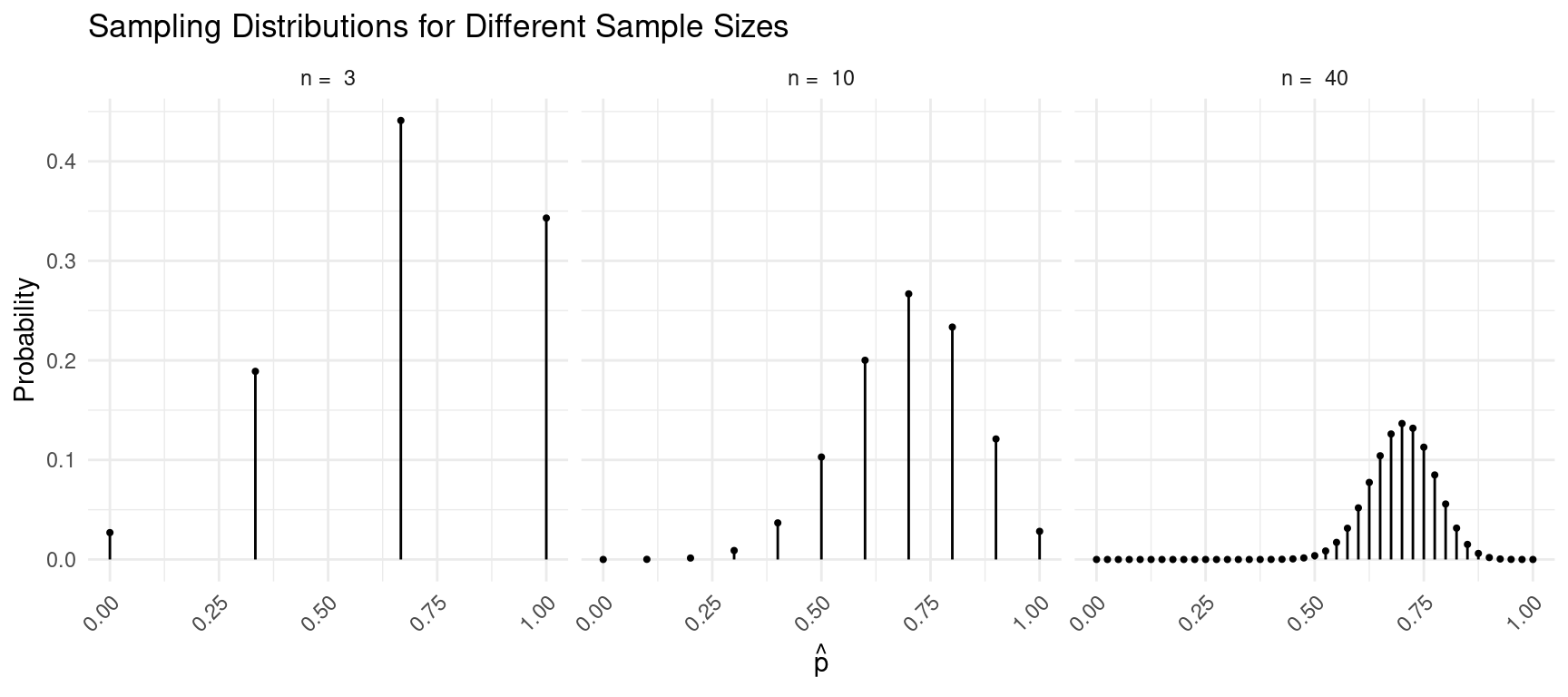
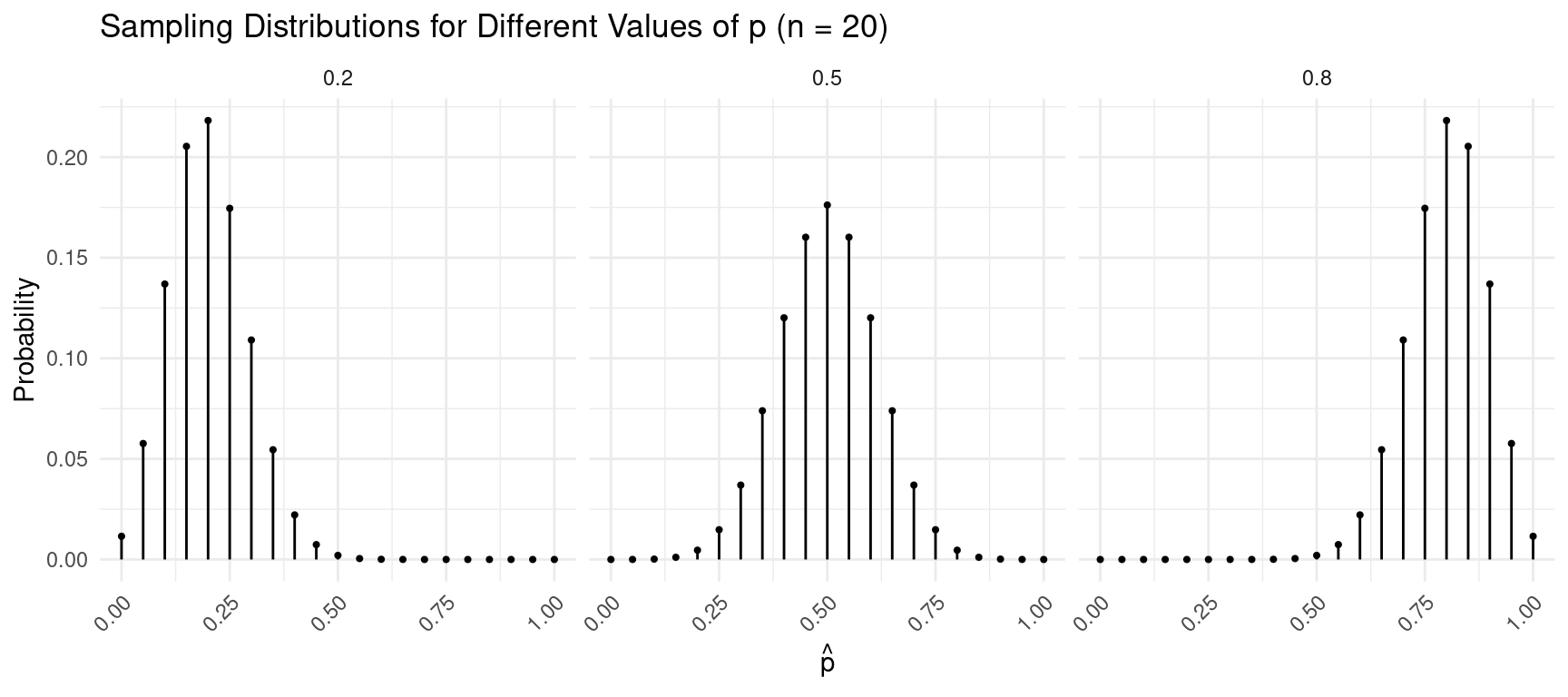
Properties of the Sampling Distribution of \(\hat{p}\)

Assume (a) that we have a population distribution where \(x\) has only two values, “success” and “failure,” and the probability of a success is \(p\), and assume (b) we observe a sample of \(n\) observations and compute the proportion (\(\hat{p}\)) of observations in the sample that are “successes.”

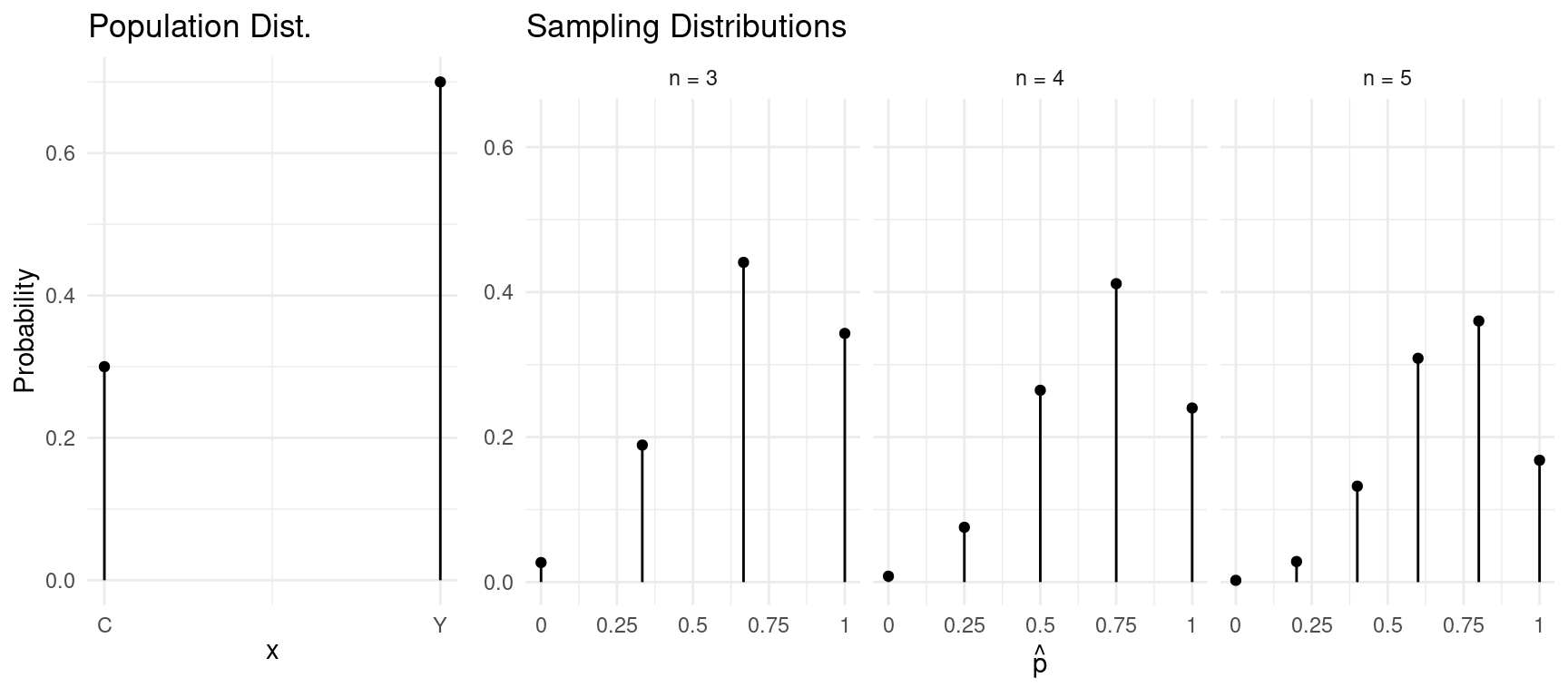
Example: Consider the following population distribution, and several sampling distributions of \(\hat{p}\) based on samples of \(n\) = 3, 4, or 5 observations.

Population Distribution
\(x\) \(P(x)\)
\(Y\) 0.7
\(C\) 0.3

Note: Here we define \(Y\) as a “success” because our proportions will be based on the number of \(Y\)’s out of \(n\).

Sampling Distribution of \(\hat{p}\), \(n\) = 3
\(\hat{p}\) \(P(\hat{p})\)
0 0.027
1/3 0.189
2/3 0.441
1 0.343

\[\begin{align*} \mu_{\hat{p}} & = 0.7 \\ \sigma_{\hat{p}} & \approx 0.26 \end{align*}\]

Sampling Distribution of \(\hat{p}\), \(n\) = 4
\(\hat{p}\) \(P(\hat{p})\)
0 0.0081
1/4 0.0756
1/2 0.2646
3/4 0.4116
1 0.2401

\[\begin{align*} \mu_{\hat{p}} & = 0.7 \\ \sigma_{\hat{p}} & \approx 0.23 \end{align*}\]

Sampling Distribution of \(\hat{p}\), \(n\) = 5
\(\hat{p}\) \(P(\hat{p})\)
0 0.00243
1/5 0.02835
2/5 0.13230
3/5 0.30870
4/5 0.36015
1 0.16807

\[\begin{align*} \mu_{\hat{p}} & = 0.7 \\ \sigma_{\hat{p}} & \approx 0.2 \end{align*}\]

Mean and Standard Deviation of \(\hat{p}\)

Assume (a) that we have a population distribution where \(x\) has only two values, “success” and “failure,” and the probability of a success is \(p\), and assume a sample of \(n\) observations.

  1. The mean of \(\hat{p}\) is \(p\) — i.e., \(\mu_{\hat{p}} = p\).
  2. The standard deviation of \(\hat{p}\) is \(\sqrt{p(1-p)/n}\) — i.e., \(\sigma_{\hat{p}} = \sqrt{p(1-p)/n}\).

Example: Assuming the population distribution given above with \(p\) = 0.7, what are the mean and standard deviation of \(\hat{p}\) based on a sample of \(n\) = 16 observations? What about \(n\) = 25 observations?

Example: Consider again the trebuchet experiment, but this time with a slightly different population distribution, which is shown below. The mean and standard deviation of \(x\) are \(\mu_x\) = 2.2 and \(\sigma_x\) \(\approx\) 0.69, respectively. A researcher would probably not know \(\mu_x\), but could estimate it by firing the trebuchet to create a sample of observations and use \(\bar{x}\) to estimate \(\mu_x\). The sampling distribution of \(\bar{x}\) based on a sample of \(n\) = 50 observations is also shown below. 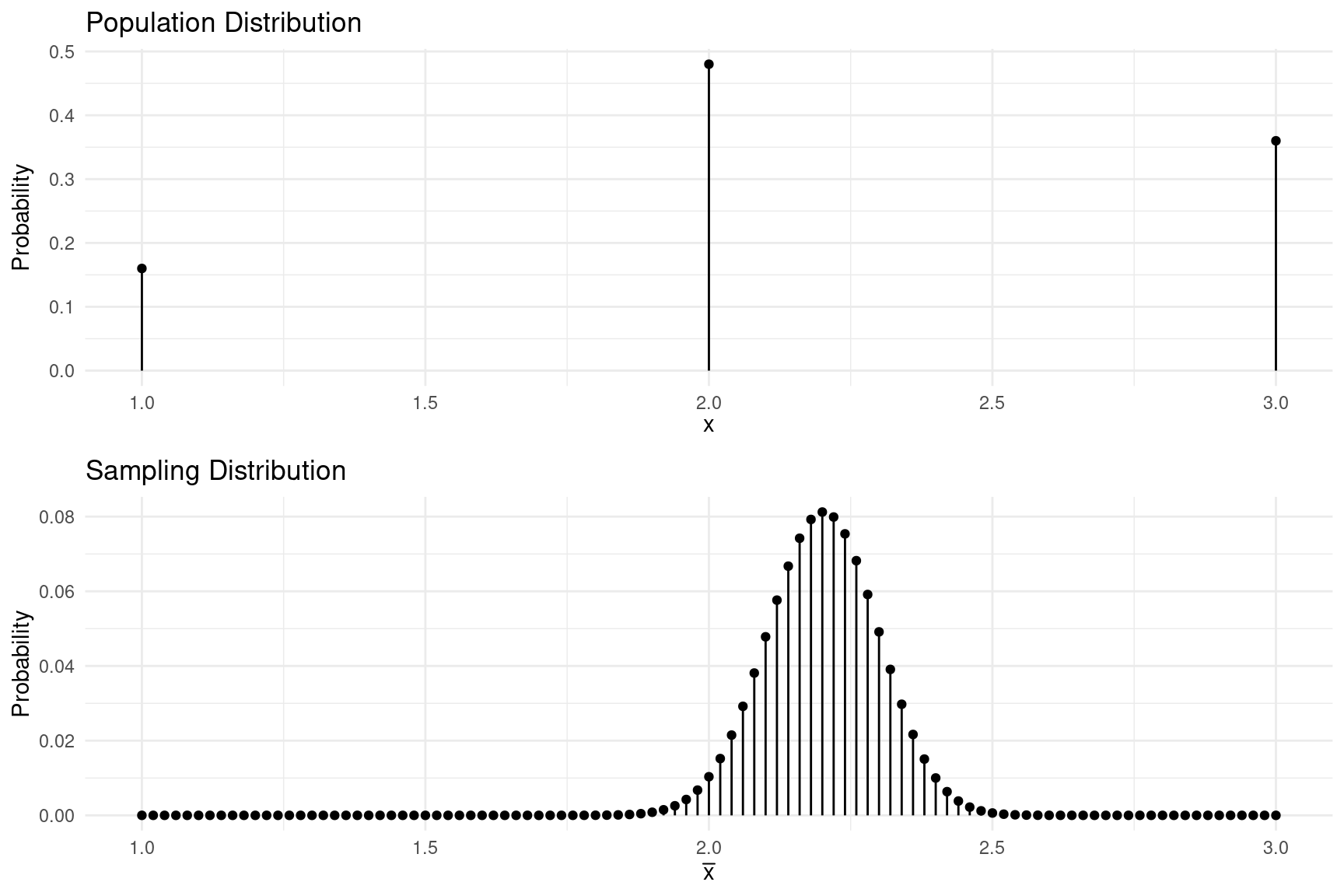What are the mean and the standard deviation of \(\bar{x}\) for such an experiment? Also what is the interval that has approximately a 0.95 probability of containing \(\bar{x}\)?

Example: Imagine a survey of fish in a lake where 20% of the fish in the lake are infected with a parasite. Let \(x\) be whether or not a randomly selected fish has a parasite. The population distribution is shown below. A researcher would probably not know that 20% of the fish in the lake are infected, but could estimate the proportion of infected fish in the lake (0.2) using the proportion of infected fish from a sample of observations (\(\hat{p}\)). The sampling distribution of \(\hat{p}\) based on a sample of \(n\) = 100 observations is also shown below. 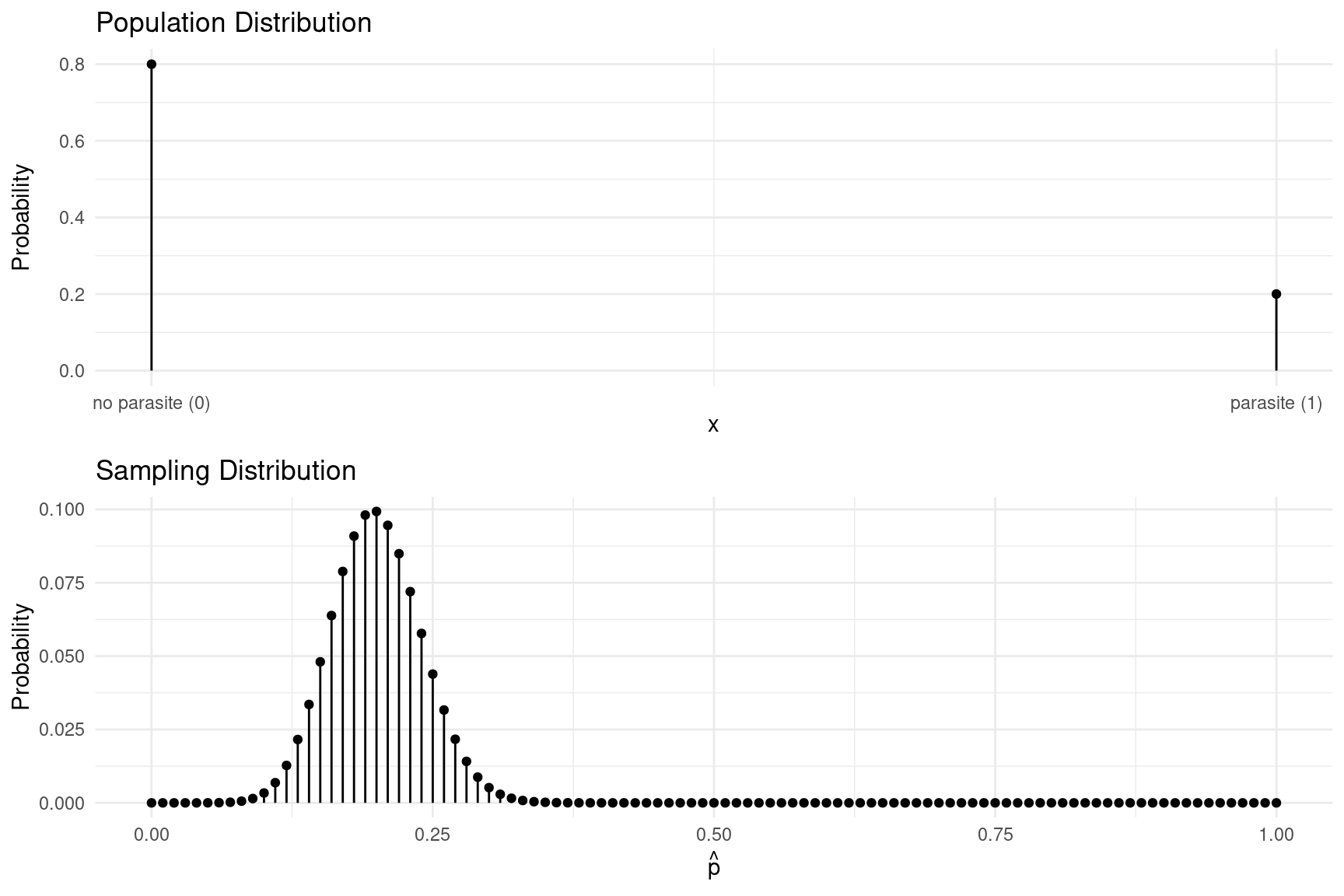What are the mean and standard deviation of \(\hat{p}\) from such a survey? Also what is the interval that has approximately a 0.95 probability of containing \(\hat{p}\)?