Wednesday, Jan 18
You can also download a PDF copy of this lecture.
Summary Measures of a Distribution — Continued
A couple of properties of a distribution that we often want to measure are location and variability.
Measures of Variability
The variance for a sample of observations can be written as \[ s^2 = \frac{(x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + \cdots + (x_n - \bar{x})^2}{n-1} = \frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n-1}. \] Example: Consider the following sample of observations: 1, 1, 7. The mean is \(\bar{x}\) = 3 and the variance is \[ s^2 = \frac{(1 - 3)^2 + (1 - 3)^2 + (7 - 3)^2}{3-1} = 12. \] A related measure is the standard deviation which is the square root of the variance, so it can be written as \[ s = \sqrt{\frac{(x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + \cdots + (x_n - \bar{x})^2}{n-1}} = \sqrt{\frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n-1}}. \] Note that the symbol for the variance is \(s^2\) because the variance equals the square of the standard deviation (\(s\)).
Another measure is the range which is simply defined as the difference between the largest and smallest values, \[ \text{range} = \max(x_1,x_2,\dots,x_n) - \min(x_1,x_2,\dots,x_n), \] and the interquartile range which we will discuss later.
Cumulative Distributions
The cumulative distribution shows the relationship between the value of the variable and cumulative relative frequency.
Example: The following is a hypothetical set of observations of examination scores.
5, 6, 6, 6, 7, 7, 8, 8, 8, 10
| \(x\) | Frequency | Relative Frequency | Cumulative Relative Frequency |
|---|---|---|---|
| 5 | 1 | 0.1 | 0.1 |
| 6 | 3 | 0.3 | 0.4 |
| 7 | 2 | 0.2 | 0.6 |
| 8 | 3 | 0.3 | 0.9 |
| 10 | 1 | 0.1 | 1.0 |
We can graph the cumulative distribution using a step
function.
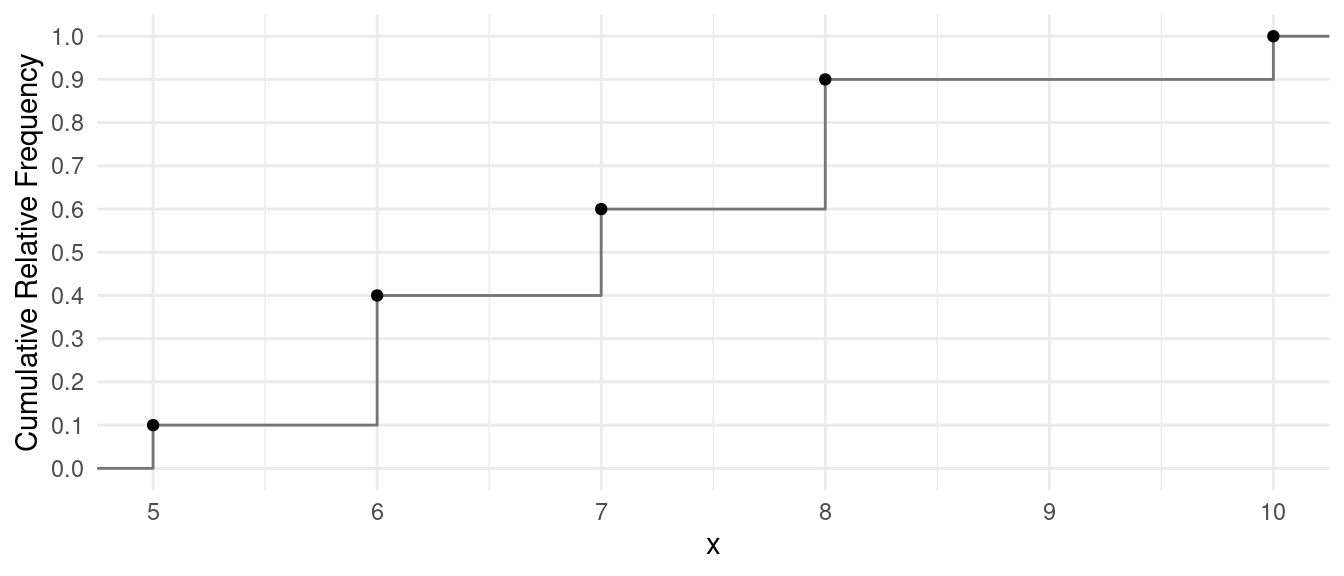
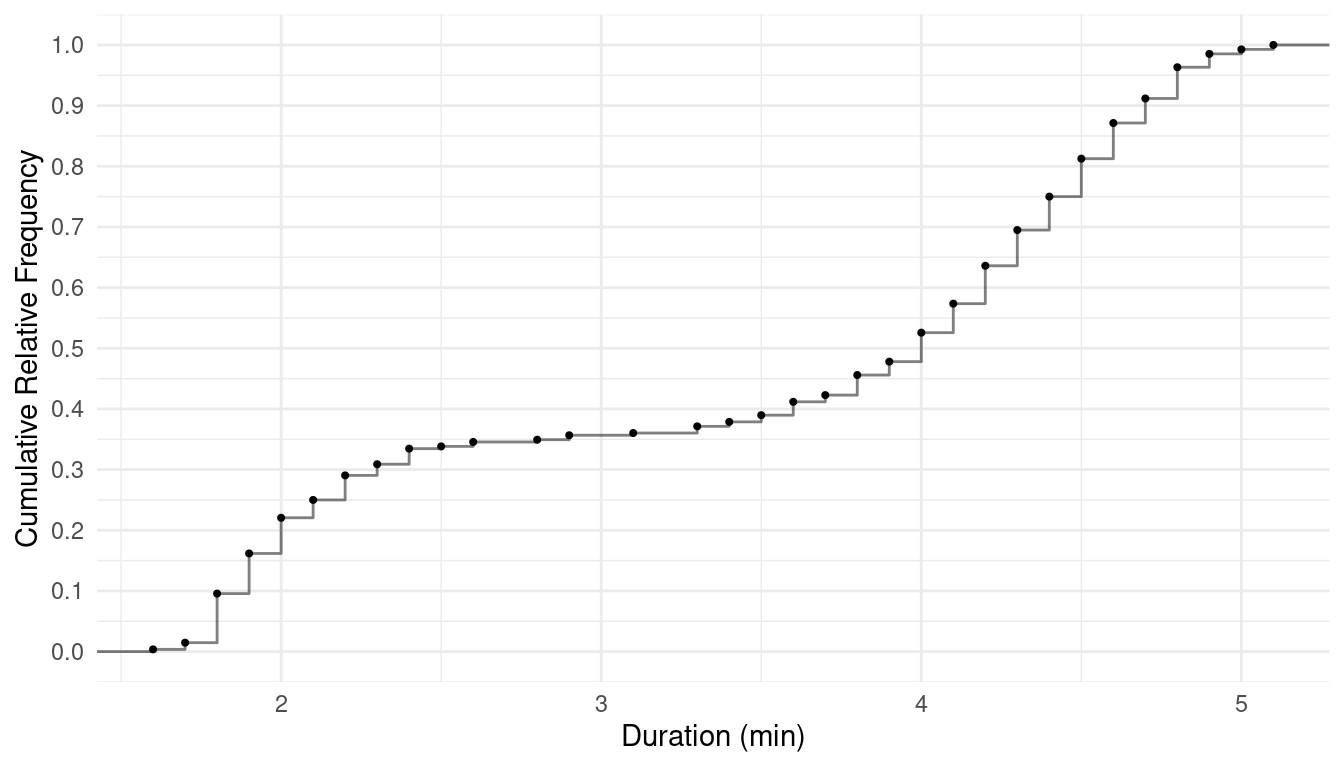
| Time | Frequency | Relative Frequency | Cumulative Relative Frequency |
|---|---|---|---|
| 1.6 | 1 | 0.004 | 0.004 |
| 1.7 | 3 | 0.011 | 0.015 |
| 1.8 | 22 | 0.081 | 0.096 |
| 1.9 | 18 | 0.066 | 0.162 |
| 2 | 16 | 0.059 | 0.221 |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| 5.1 | 2 | 0.007 | 1 |
Note: The relative and cumulative relative frequencies above have
been rounded.
Finding Percentiles Using a Cumulative Distribution
The \(P\)th percentile is the value of the variable such that \(P\%\) of the observations are less than that value.
Finding Percentiles: Finding percentiles from a set of observations is surprisingly complex! Consider the following distribution.| \(x\) | Frequency | Relative Frequency | Cumulative Relative Frequency |
|---|---|---|---|
| 5 | 1 | 0.1 | 0.1 |
| 6 | 3 | 0.3 | 0.4 |
| 7 | 2 | 0.2 | 0.6 |
| 8 | 3 | 0.3 | 0.9 |
| 10 | 1 | 0.1 | 1.0 |
Here are a couple of examples.
What is the 60th percentile? Several values of \(x\) would qualify! Any \(x\) such that 7 \(<\) x \(\le\) 8 has 60% of the observations that are less than it.
What is the 70th percentile? No values of \(x\) would qualify! The percent of observations less than 8 is 60%, and the percent of observations for any \(x\) > 8 is 90% or more.
One solution is to use the midpoint in the first case, and the smallest value of \(x\) that has more than \(P\)% of observations less than it in the second case. This is easier to explain/do using a graph of the cumulative distribution.
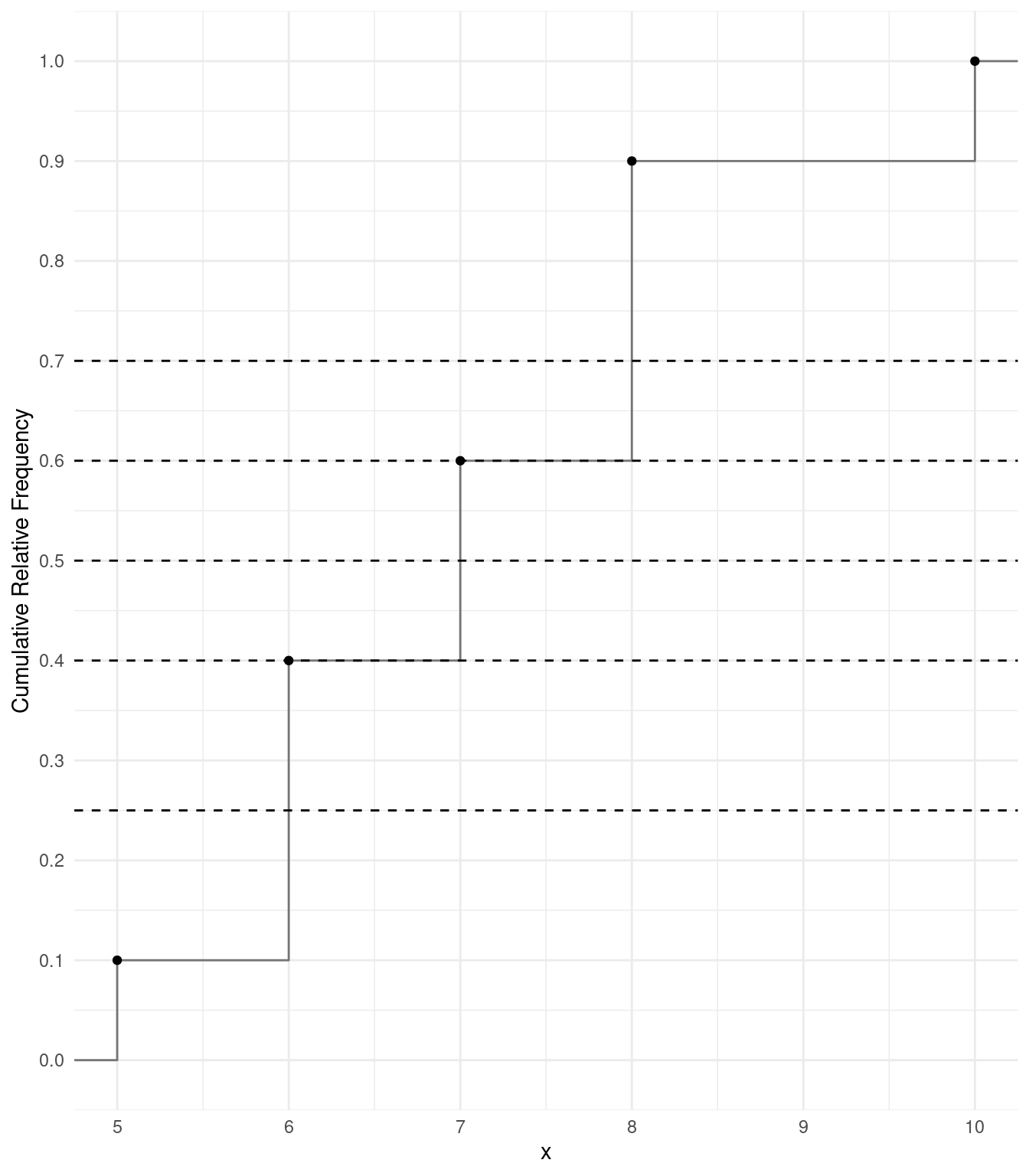
Finding Percentiles Using the Cumulative Distribution: To find the approximate percentile using a graph of the cumulative relative distribution, find the value where the step function crosses the cumulative relative frequency of \(P\)/100. If more than one value crosses value, use the midpoint (i.e., average of the two values).
Example: We can confirm that the 25th, 40th, 50th, 60th, and 70th percentiles for the distribution show below are 6, 6.5, 7, 7.5, and 8, respectively.
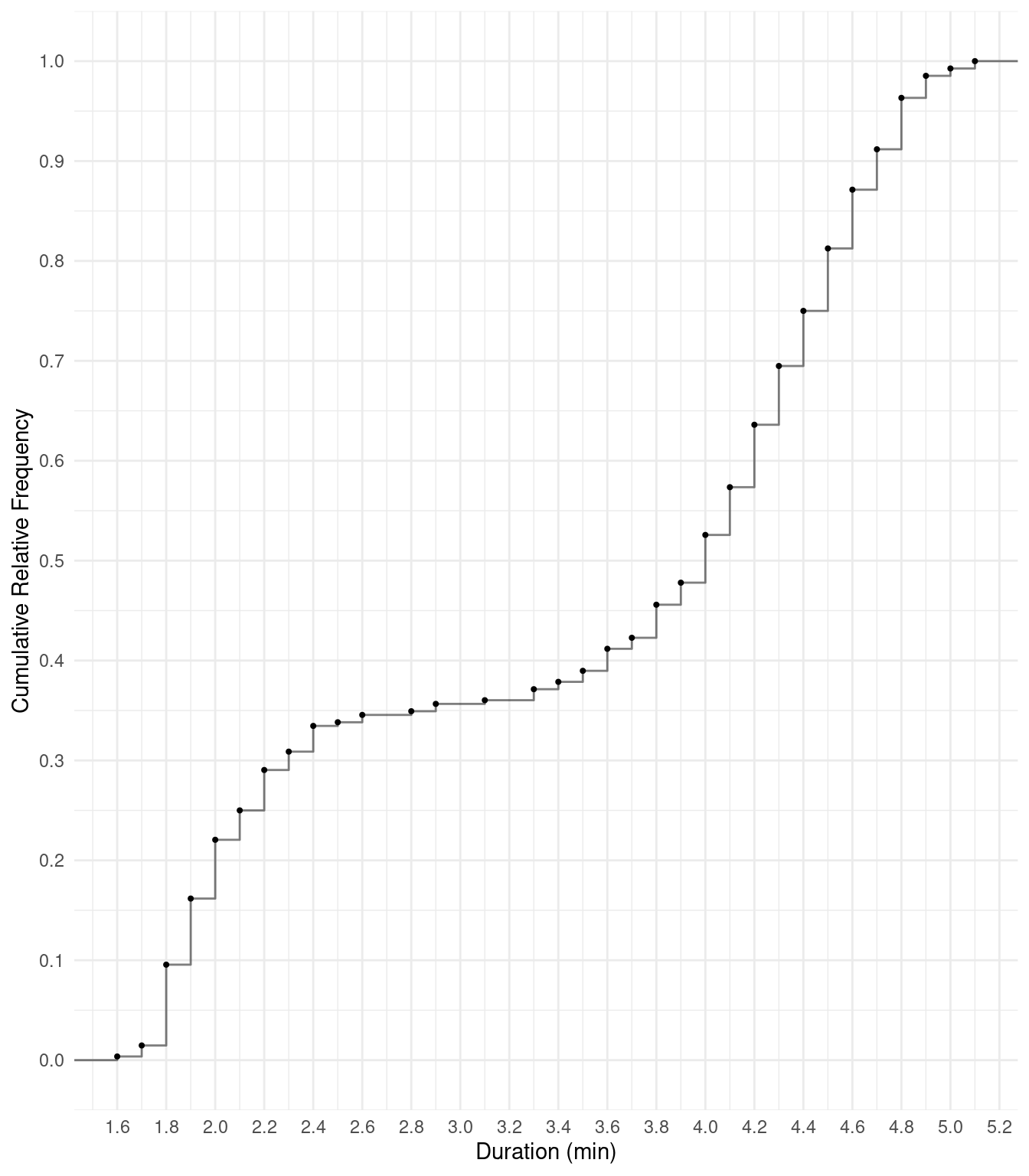
Example: We can use the following plot to
approximate the 25th, 50th, and 75th percentiles “by eye” (the actual
percentiles are 2.15, 4, and 4.45).
Box Plots
A box plot is a graphical representation of a distribution of a quantitative variable that uses what is called a five-number summary:
- minimum
- first quartile (\(Q_1\)) — i.e., 25th percentile
- second quartile (\(Q_2)\) — i.e., 50th percentile and median
- third quartile (\(Q_3\)) — i.e., 75th percentile
- maximum
Comment: Because there is more than one way to approximate a percentile and thus a quartile, there is more than one way to draw a boxplot. For consistency we will use the approximation given earlier for finding percentiles.
Example: Box plot based on an earlier example.
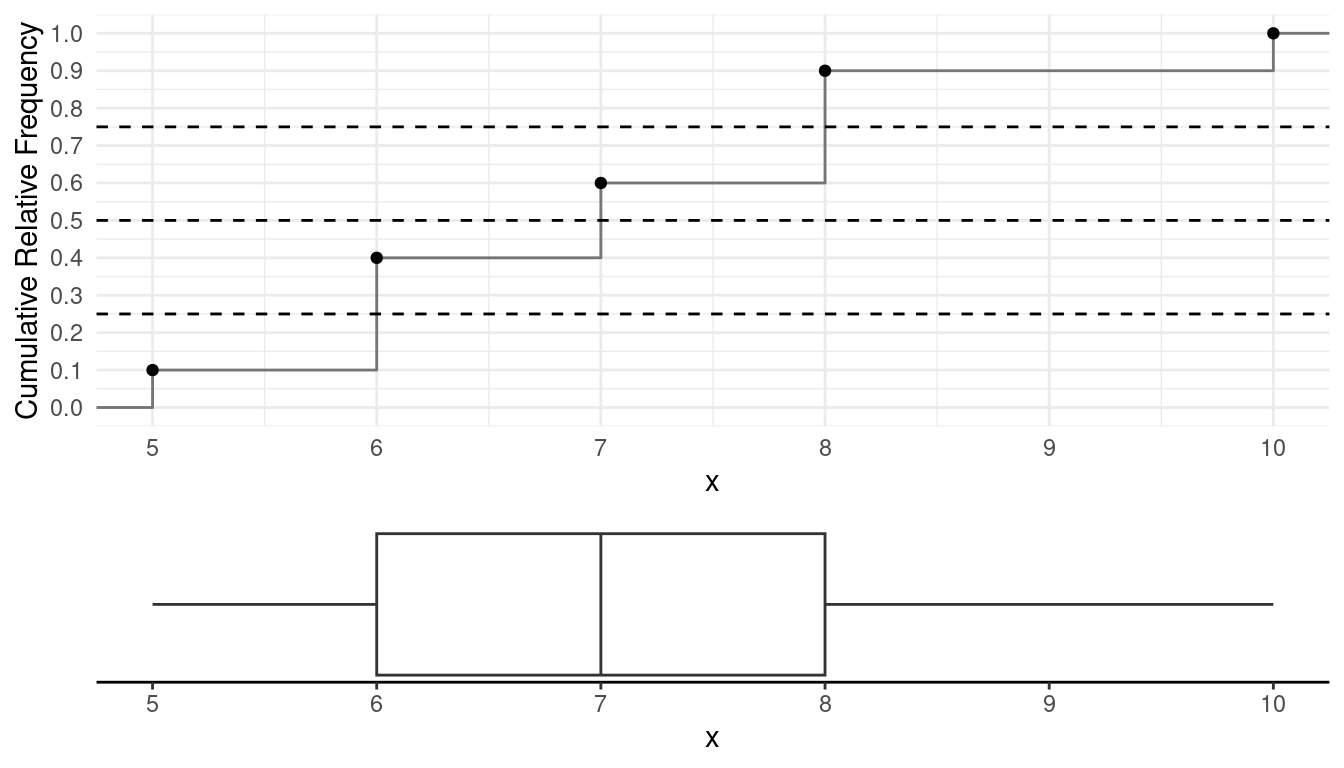 Note that the five number summary is 5, 6, 7, 8, and 10.
Note that the five number summary is 5, 6, 7, 8, and 10.
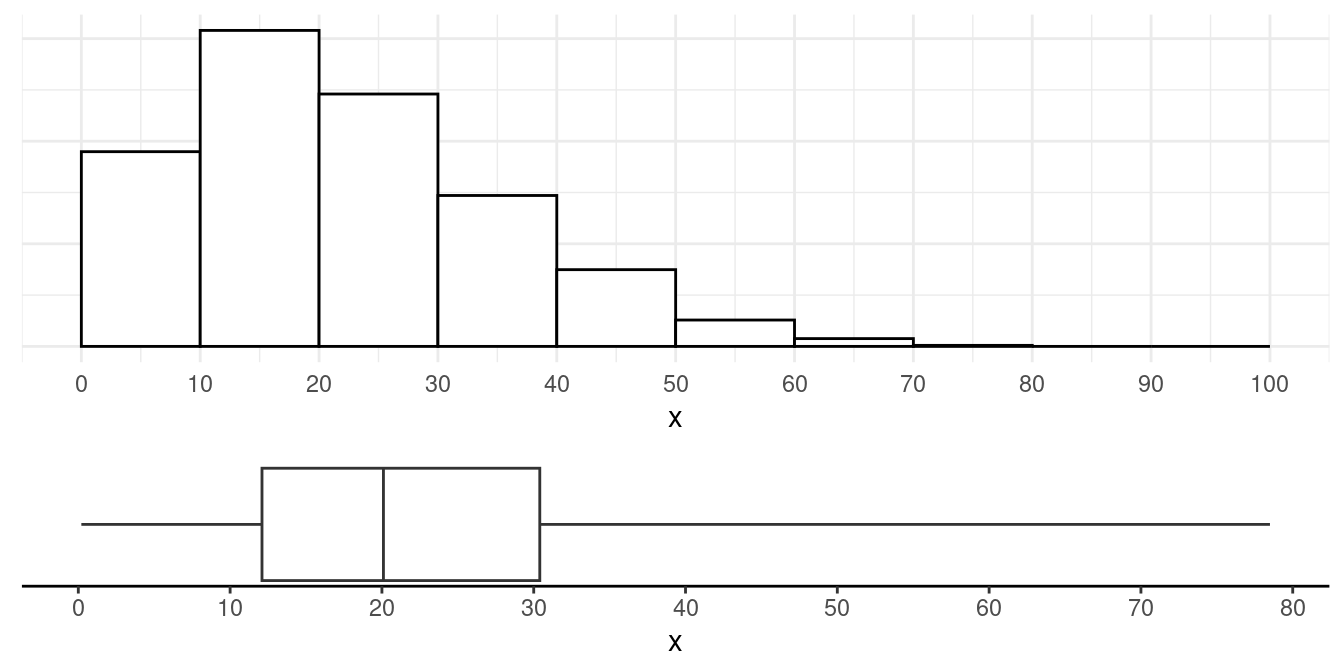
Example: Box plot of the Old Faithful data.
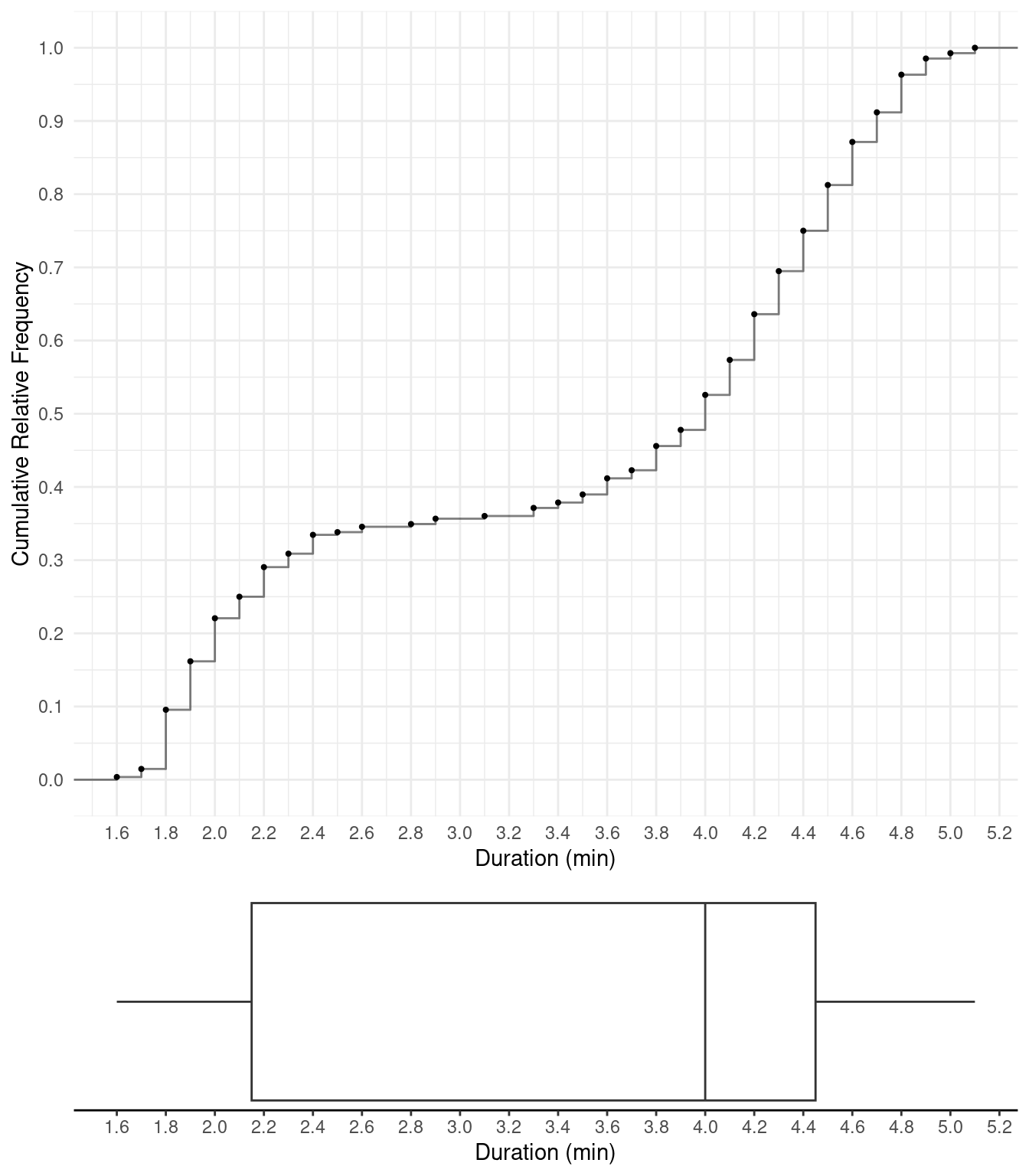 Note that the five number summary is 1.6, 2.15, 4, 4.45, and 5.1.
Note that the five number summary is 1.6, 2.15, 4, 4.45, and 5.1.
A box plot visually depicts three summary measures: the median (i.e., \(Q_2\)), range (i.e., maximum \(-\) minimum), and interquartile range (i.e., \(Q_3-Q_1\)).
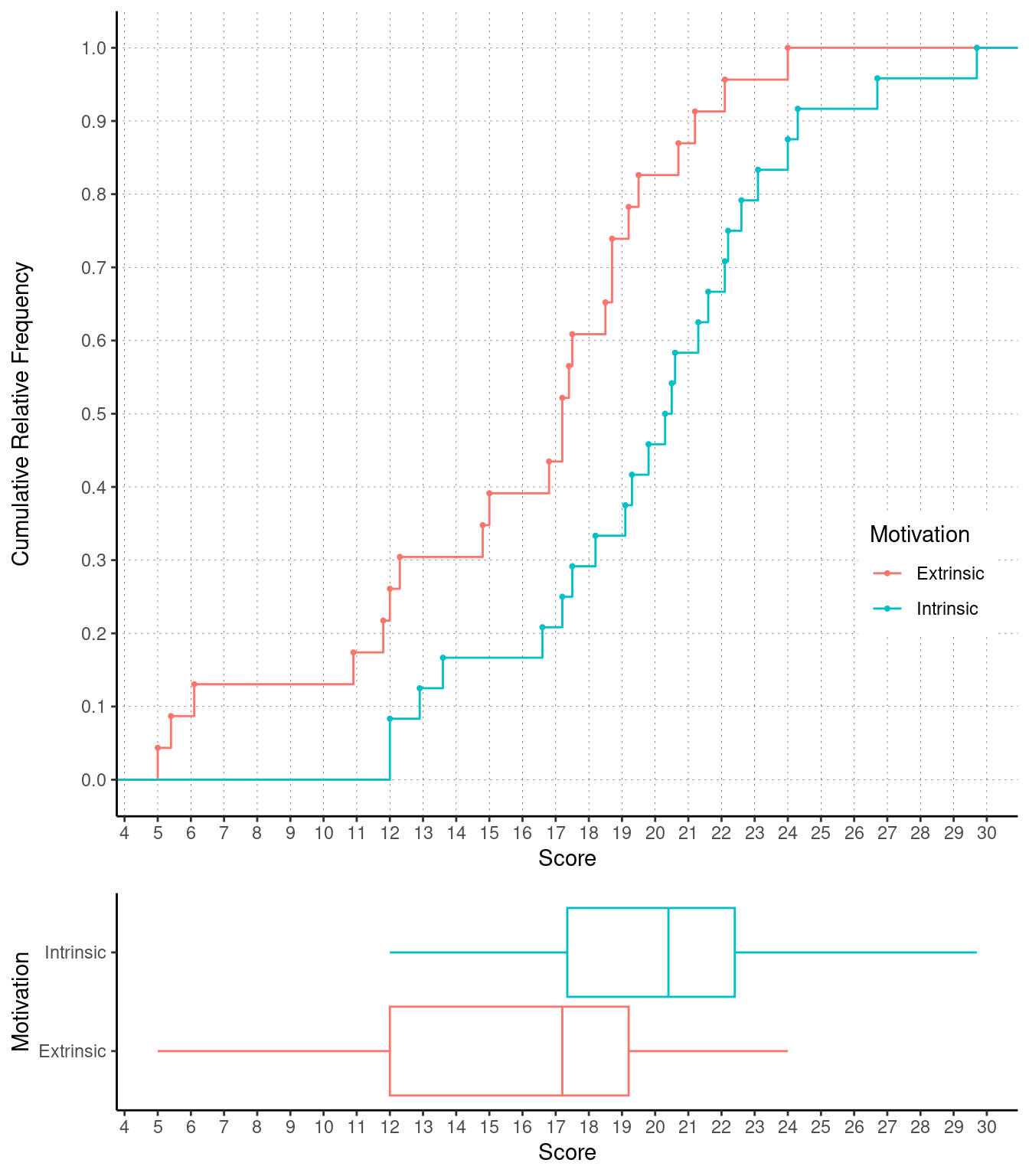
Example: Cumulative distributions and box plots of
the data from the study on creativity and motivation.
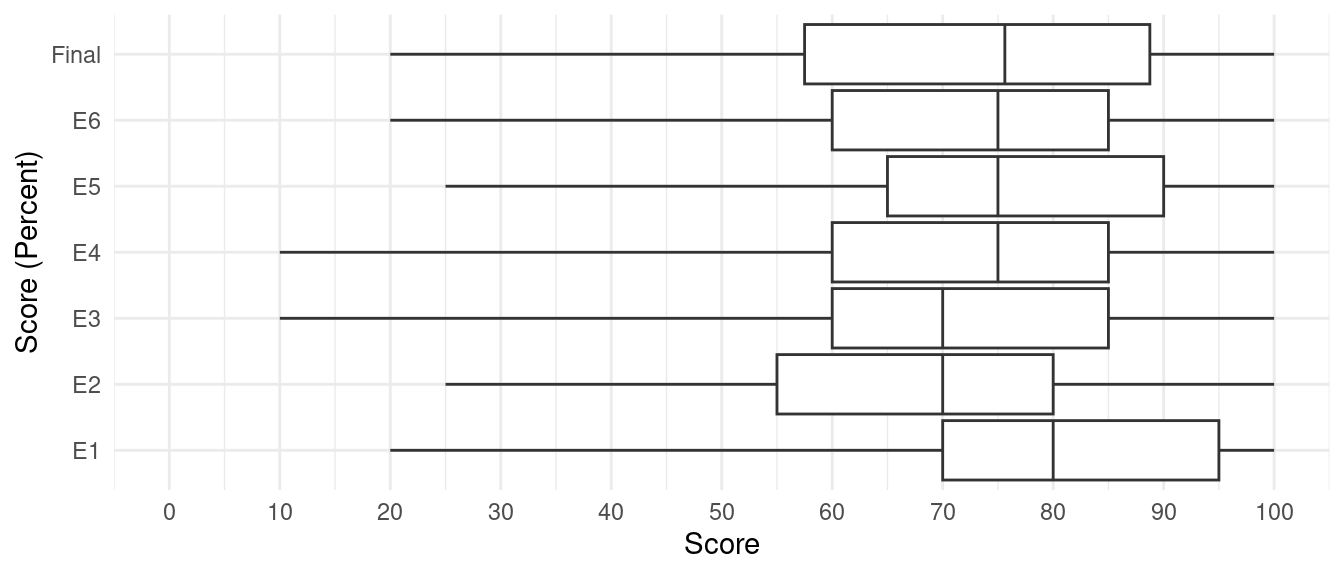
Example: Distribution of examination scores from
Stat 251, Fall 2016.
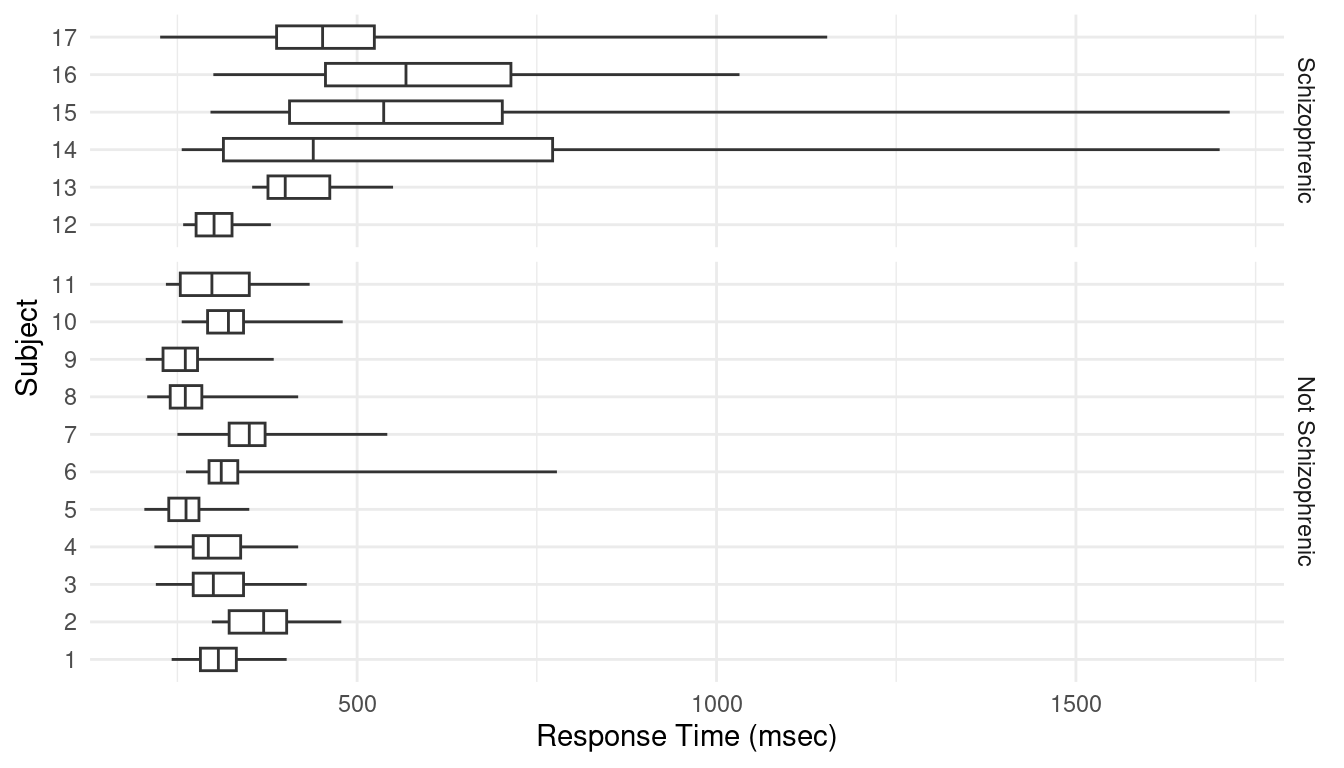
Example: Distribution of response times for 11
non-schizophrenic individuals and six schizophrenic individuals.
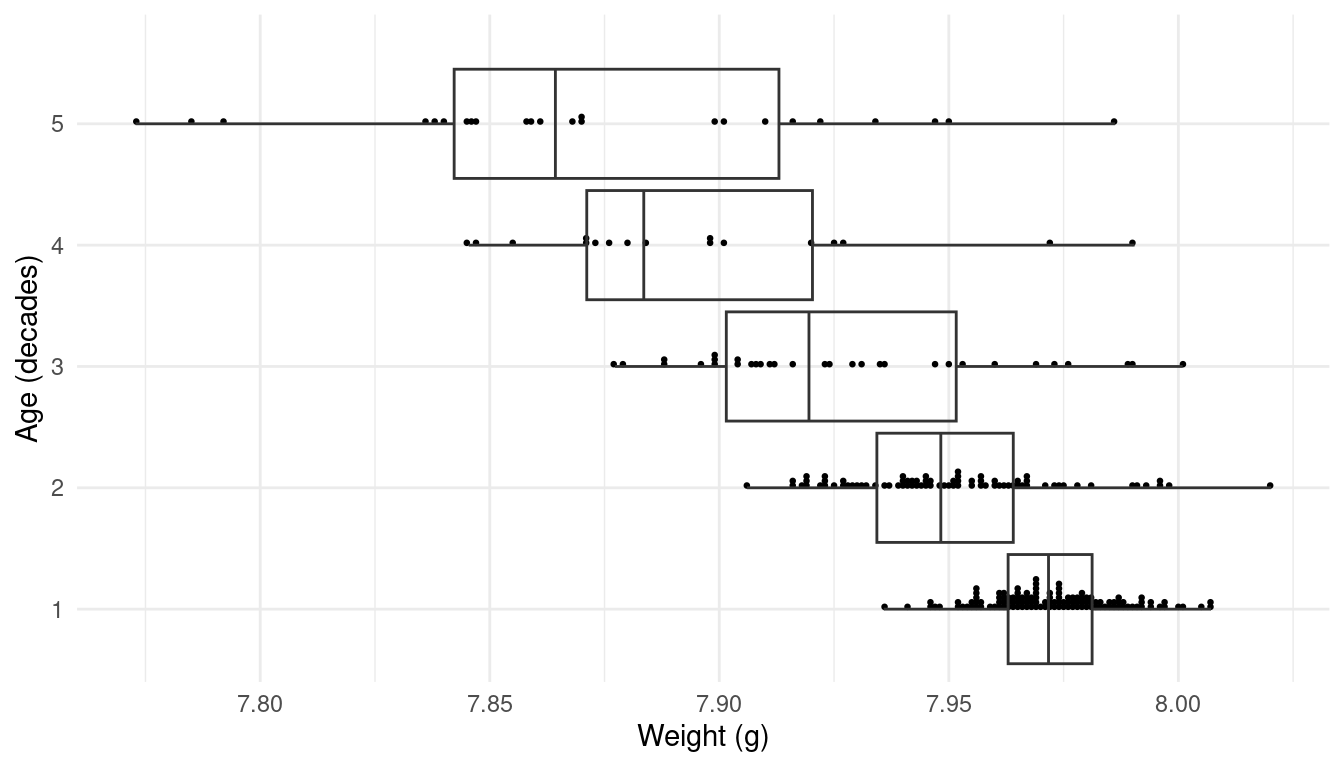
| Age | n | mean | sd | min | Q1 | Q2 | Q3 | max | IQR |
|---|---|---|---|---|---|---|---|---|---|
| 5 | 24 | 7.873 | 0.0535 | 7.773 | 7.842 | 7.864 | 7.913 | 7.986 | 0.0708 |
| 4 | 17 | 7.896 | 0.0406 | 7.845 | 7.871 | 7.883 | 7.920 | 7.990 | 0.0492 |
| 3 | 32 | 7.928 | 0.0343 | 7.877 | 7.902 | 7.920 | 7.952 | 8.001 | 0.0501 |
| 2 | 78 | 7.950 | 0.0227 | 7.906 | 7.934 | 7.948 | 7.964 | 8.020 | 0.0297 |
| 1 | 123 | 7.973 | 0.0141 | 7.936 | 7.963 | 7.972 | 7.981 | 8.007 | 0.0183 |
Distribution Shapes
Some terms we use to describe the shape of the distribution of a quantitative variable: symmetric, uniform, left-skewed, right-skewed, uni-modal, bi-modal.
Example: Uniform and symmetric.
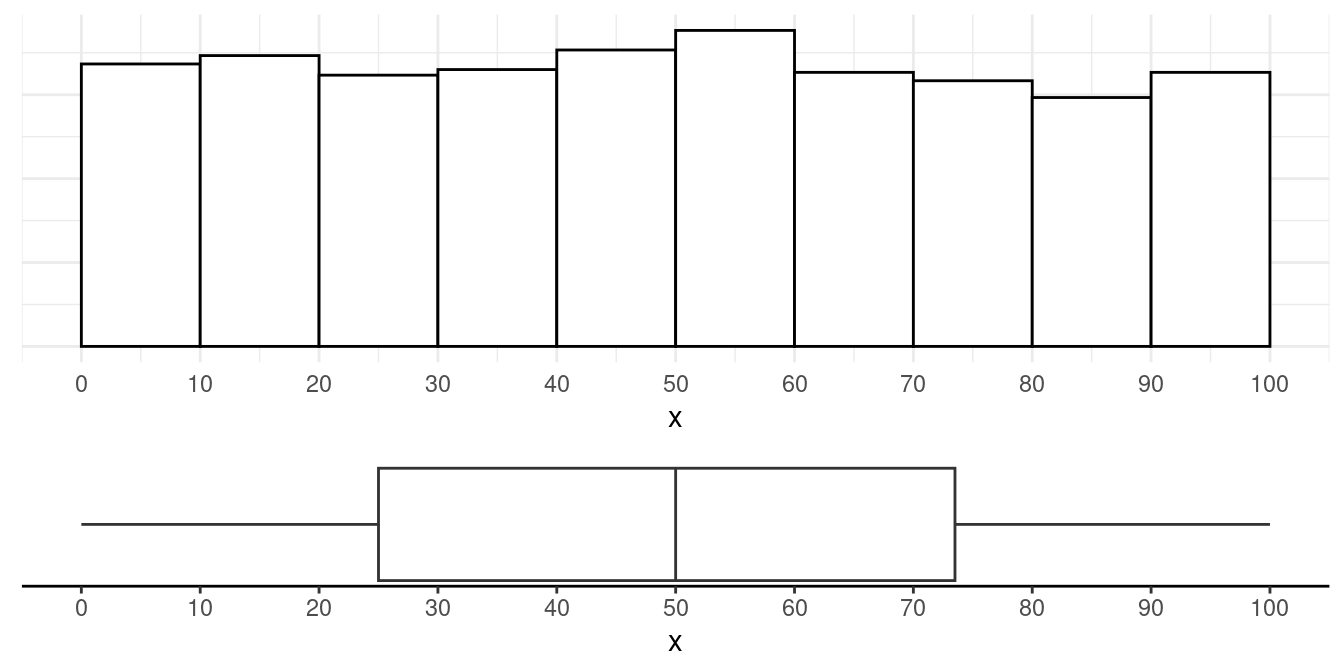
Example: Uni-modal and symmetric.
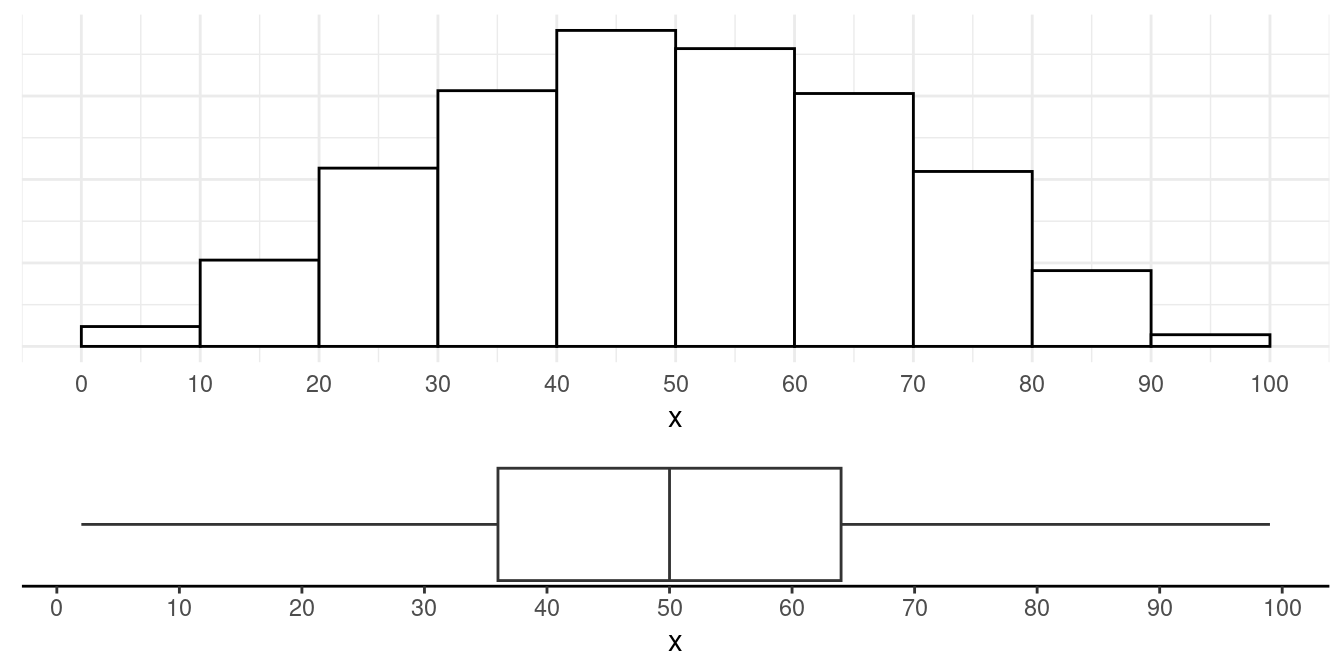
Example: Bi-modal and symmetric.
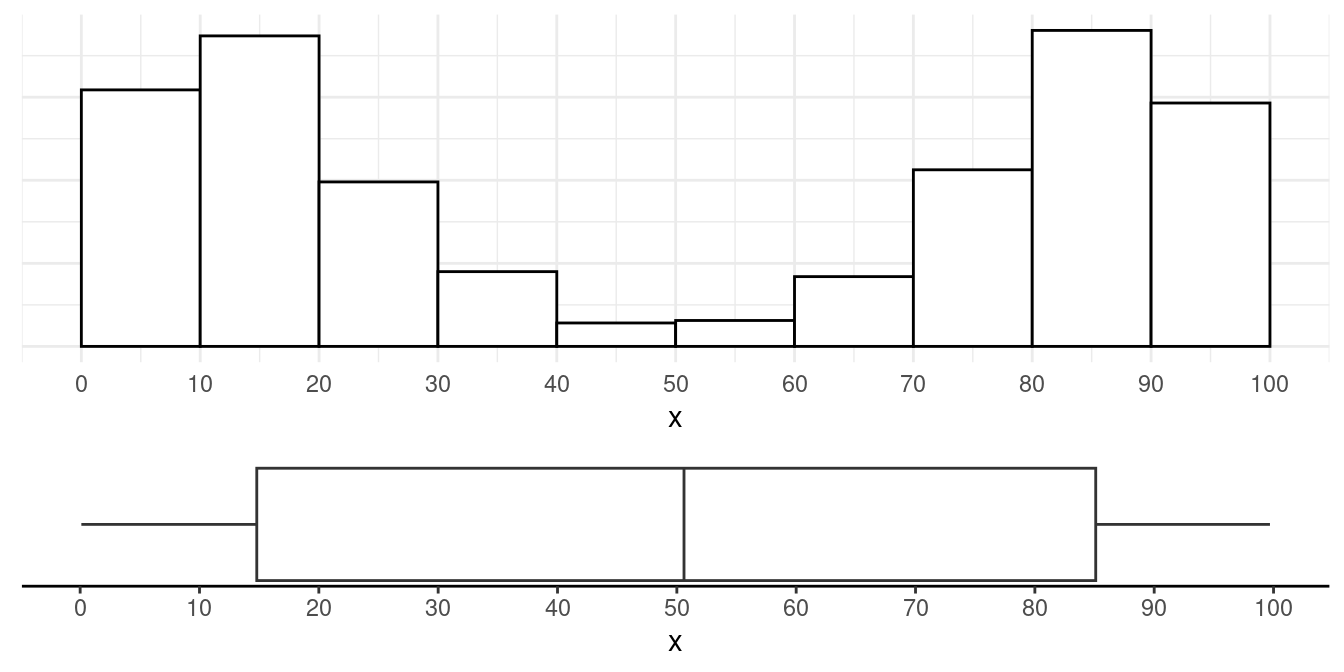
Example: Left-skewed and uni-modal.
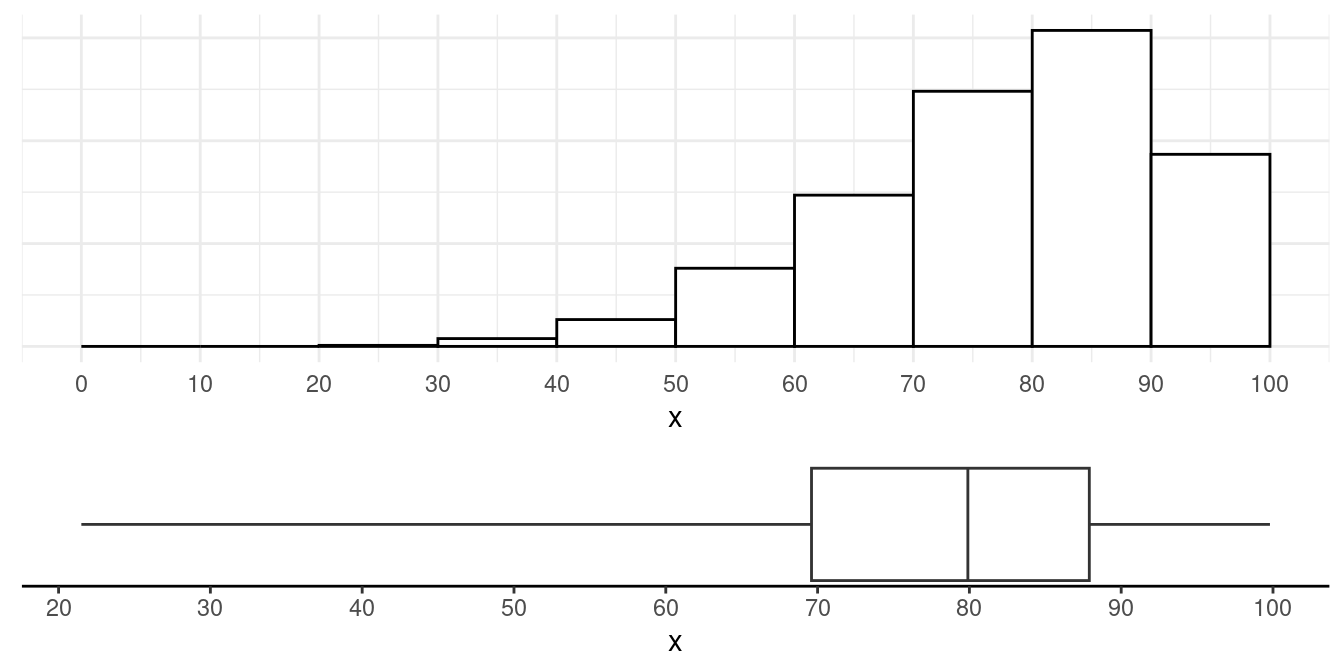
Example: Right-skewed and uni-modal.