You can also download a PDF copy of this lecture.

Sampling Distributions — Continued

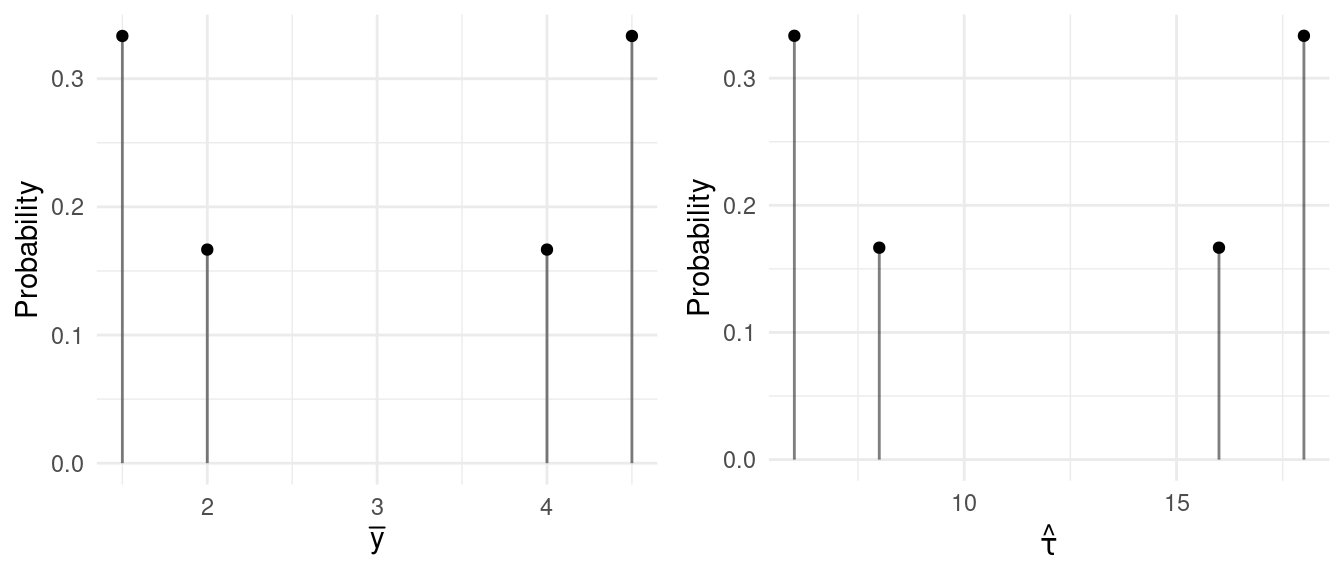
Example: Suppose we have a population of \(N\) = 4 elements where the target variable values are 1, 2, 2, and 7. The table below shows the sample space for a simple random sampling design with \(n\) = 2 as well as the values of the estimators. \(\hat\tau\) and \(\bar{y}\) for each sample.
Sample \(\hat\tau\) \(\bar{y}\)
\(\{\mathcal{E}_{1},\mathcal{E}_{2}\}\) 6 1.5
\(\{\mathcal{E}_{1},\mathcal{E}_{3}\}\) 6 1.5
\(\{\mathcal{E}_{1},\mathcal{E}_{4}\}\) 16 4.0
\(\{\mathcal{E}_{2},\mathcal{E}_{3}\}\) 8 2.0
\(\{\mathcal{E}_{2},\mathcal{E}_{4}\}\) 18 4.5
\(\{\mathcal{E}_{3},\mathcal{E}_{4}\}\) 18 4.5
Note that a sample space is simply the set of all possible samples. Here there are 6 samples in the sample space. The table below shows the sampling distributions of \(\bar{y}\) and \(\hat\tau\).
\(\bar{y}\) \(\hat\tau\) Probability
1.5 6 1/3
2.0 8 1/6
4.0 16 1/6
4.5 18 1/3

The figures below show the sampling distributions of \(\bar{y}\) and \(\hat\tau\).

Example: Suppose now we have a population of \(N\) = 10 elements where the target variable values are 2, 3, 3, 4, 5, 6, 6, 9, 10, and 10. The table below shows the (abbreviated) sample space for a simple random sampling design with \(n\) = 4 as well as the values of the estimators \(\hat\tau\) and \(\bar{y}\) for each sample.
Sample \(\hat\tau\) \(\bar{y}\)
\(\{\mathcal{E}_{1},\mathcal{E}_{2},\mathcal{E}_{3},\mathcal{E}_{4}\}\) 30 3
\(\{\mathcal{E}_{1},\mathcal{E}_{2},\mathcal{E}_{3},\mathcal{E}_{5}\}\) 32.5 3.25
\(\{\mathcal{E}_{1},\mathcal{E}_{2},\mathcal{E}_{3},\mathcal{E}_{6}\}\) 35 3.5
\(\{\mathcal{E}_{1},\mathcal{E}_{2},\mathcal{E}_{3},\mathcal{E}_{7}\}\) 35 3.5
\(\{\mathcal{E}_{1},\mathcal{E}_{2},\mathcal{E}_{3},\mathcal{E}_{8}\}\) 42.5 4.25
\(\{\mathcal{E}_{1},\mathcal{E}_{2},\mathcal{E}_{3},\mathcal{E}_{9}\}\) 45 4.5
\(\{\mathcal{E}_{1},\mathcal{E}_{2},\mathcal{E}_{3},\mathcal{E}_{10}\}\) 45 4.5
\(\{\mathcal{E}_{1},\mathcal{E}_{2},\mathcal{E}_{4},\mathcal{E}_{5}\}\) 35 3.5
\(\vdots\) \(\vdots\) \(\vdots\)
\(\{\mathcal{E}_{7},\mathcal{E}_{8},\mathcal{E}_{9},\mathcal{E}_{10}\}\) 87.5 8.75
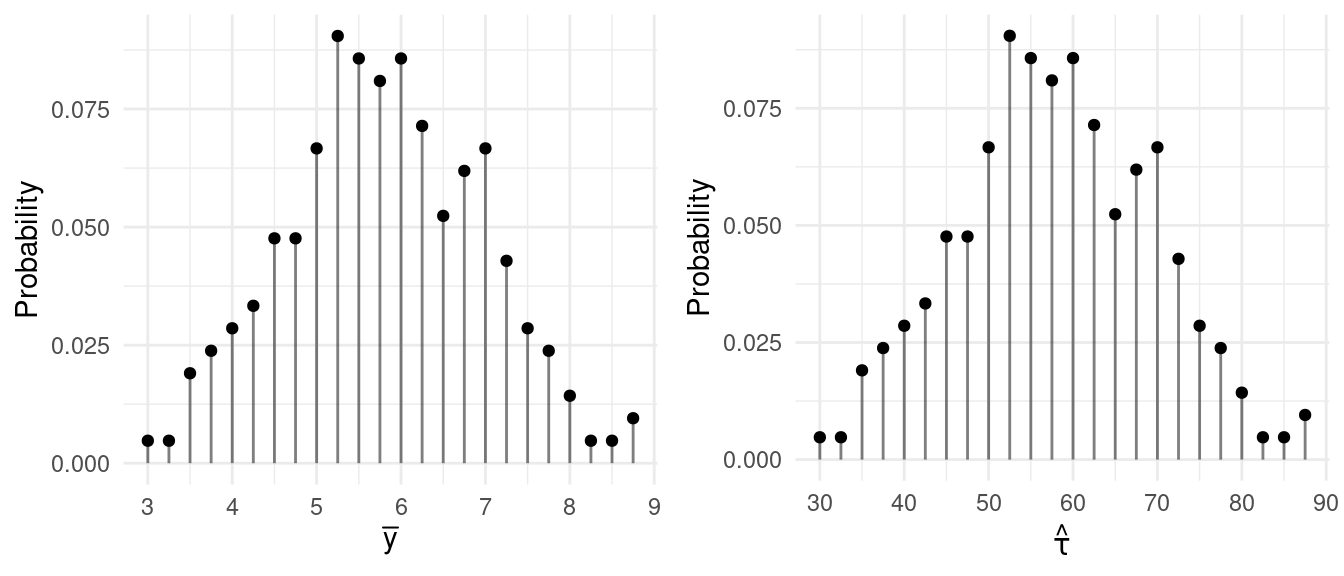
Here there are 210 samples in the sample space. The table below shows the sampling distributions of \(\bar{y}\) and \(\hat\tau\).
\(\bar{y}\) \(\hat\tau\) Probability
3.00 30.0 0.0047619
3.25 32.5 0.0047619
3.50 35.0 0.0190476
3.75 37.5 0.0238095
4.00 40.0 0.0285714
4.25 42.5 0.0333333
4.50 45.0 0.0476190
4.75 47.5 0.0476190
5.00 50.0 0.0666667
5.25 52.5 0.0904762
5.50 55.0 0.0857143
5.75 57.5 0.0809524
6.00 60.0 0.0857143
6.25 62.5 0.0714286
6.50 65.0 0.0523810
6.75 67.5 0.0619048
7.00 70.0 0.0666667
7.25 72.5 0.0428571
7.50 75.0 0.0285714
7.75 77.5 0.0238095
8.00 80.0 0.0142857
8.25 82.5 0.0047619
8.50 85.0 0.0047619
8.75 87.5 0.0095238

The figures below show the sampling distributions of \(\bar{y}\) and \(\hat\tau\).

Means and Variances of Random Variables

If we have a discrete random variable \(X\), then the mean of that random variable (also called its expectation or expected value) is \[ E(X) = \sum_x xP(x), \] where the \(x\) below \(\sum\) indicates that we sum over all values of \(x\).

Example: We can easily confirm that based on the sampling distributions for the smaller population above that \(E(\bar{y}) =\) 3 and \(E(\hat\tau) =\) 12.

But there is a shortcut if we use simple random sampling. For any simple random sampling design, it can be shown that \(E(\bar{y}) = \mu\) and \(E(\hat\tau) = \tau\). When the mean of an estimator equals what is being estimated, then we say that the estimator is an unbiased estimator (otherwise the estimator is a biased estimator).1

Warning: We have discussed two distinct means here: the population mean (\(\mu\)), and the mean of an estimator — e.g., \(E(\bar{y})\) and \(E(\hat\tau)\). Don’t confuse them!

If we have a discrete random variable \(X\), then the variance of that random variable is \[ \text{V}(X) = \sum_x [x - E(X)]^2P(x). \] Example: We can easily confirm that based on the sampling distributions for the smaller population above that \(\text{V}(\bar{y}) \approx\) 1.83 and \(\text{V}(\hat\tau) \approx\) 29.33.

It can be shown that under simple random sampling that the variances can be computed as \[ \text{V}(\bar{y}) = \left(1 - \frac{n}{N}\right)\frac{\sigma^2}{n} \ \ \ \text{and} \ \ \ \text{V}(\hat\tau) = N^2\left(1 - \frac{n}{N}\right)\frac{\sigma^2}{n}, \] where \(\sigma^2\) is the population variance \[ \sigma^2 = \frac{1}{N-1}\sum_{i=1}^N(y_i - \mu)^2, \] and where \(\mu\) is the population mean.2

Example: For the smaller population above \(\sigma^2 =\) 7.33, and for the larger population \(\sigma^2 \approx\) 8.84. What are \(\text{V}(\bar{y})\) and \(\text{V}(\hat\tau)\) for each design?

Warning: We’ve discussed two distinct variances here: the population variance (\(\sigma^2\)) and the variance of an estimator — e.g., \(\text{V}(\bar{y})\) and \(\text{V}(\hat\tau)\). Don’t confuse them!

How do \(n\) and \(N\) affect the variance of these estimators?

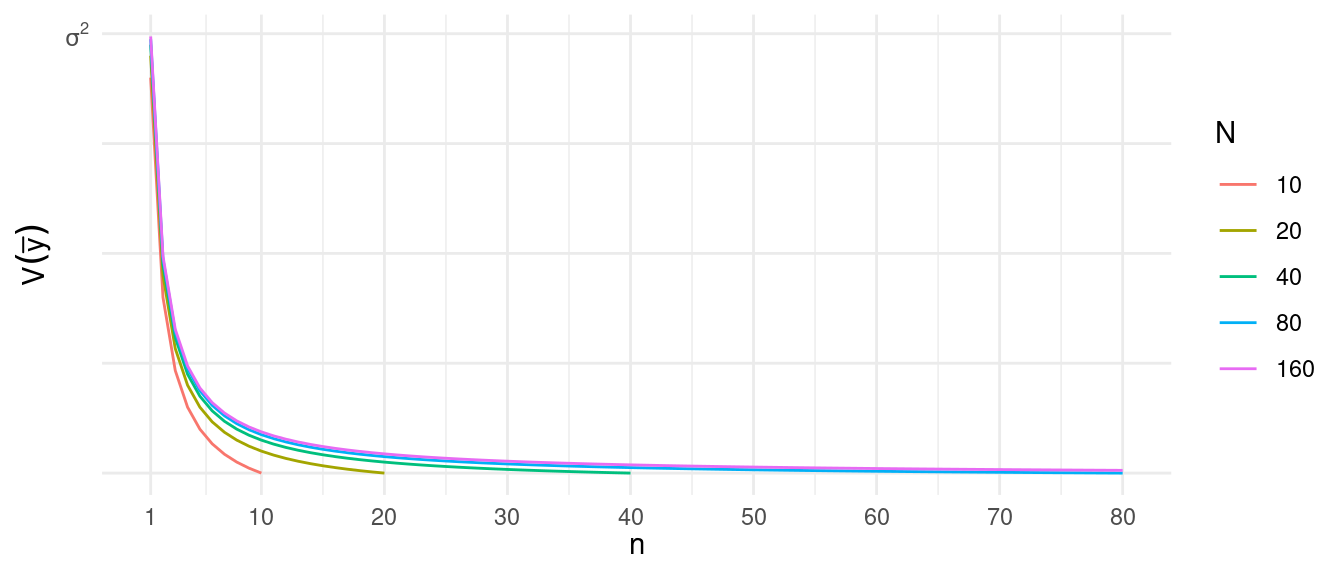
The finite population correction (FPC) is the term \(1 - n/N\) in \[ \text{V}(\bar{y}) = \left(1 - \frac{n}{N}\right)\frac{\sigma^2}{n} \ \ \ \text{and} \ \ \ \text{V}(\hat\tau) = N^2\left(1 - \frac{n}{N}\right)\frac{\sigma^2}{n}. \] The term \(n/N\) is the sampling fraction (i.e., the fraction of elements in the population that are in the sample).

  1. When is the finite population correction largely “irrelevant” to the variance of \(\bar{y}\) or \(\hat\tau\)?

  2. A census is when every element in the population is included within the sample so that \(n = N\). What happens to the variance of our estimators in a census?

  3. In practice we sometimes do not know \(N\). What can we do in these situations?

  1. The proof that \(\hat\tau\) is unbiased is not very complicated. We need to show that \(E(\hat\tau) = \tau\). Note that we can write \(\hat\tau\) a different way as \[ \hat\tau = \frac{N}{n}\sum_{i=1}^N Z_iy_i \] where \(Z_i = 1\) if the \(i\)-th element in the population is included in the sample, and \(Z_i = 0\) otherwise. Now we need to show that \[ E(\hat\tau) = E\left(\frac{N}{n}\sum_{i=1}^NZ_iy_i\right). \] From the properties of expectations we can write this as \[ E(\hat\tau) = \frac{N}{n}\sum_{i=1}^NE(Z_i)y_i. \] Now \(Z_i\) has what is sometimes called a Bernoulli distribution, and it can be shown that \(E(Z_i) = P(Z_i = 1)\) which we know is the inclusion probability, \(n/N\), since \(Z_i = 1\) if and only if the \(i\)-th element is included in the sample. So we have \[ E(\hat\tau) = \frac{N}{n}\sum_{i=1}^N\frac{n}{N}y_i = \sum_{i=1}^N y_i = \tau. \] Note that \(\sum_{i=1}^N \frac{n}{N} y_i = \frac{n}{N}\sum_{i=1}^N y_i\). Also it can be shown that this result implies that \(E(\bar{y}) = \mu\).↩︎

  2. The proof that these are the variances of \(\bar{y}\) and \(\hat\tau\) are a bit more involved than that of the unbiasedness of \(\bar{y}\) and \(\hat\tau\), but I can show them to you if you are interested. Some textbooks will define \(\sigma^2\) by dividing by \(N\) instead of \(N-1\). This can be done but it changes the formulas for \(V(\bar{y})\) and \(V(\hat\tau)\) in a way that I find awkward for later developments. In terms of our interpretation of \(\sigma^2\) this is inconsequential since we rarely care about \(\sigma^2\) in isolation and the difference between \(N\) and \(N-1\) is very small when \(N\) is large which is frequently the case in survey sampling.↩︎