Homework Problem Set 13: Inferences for \(p_1-p_2\) from Independent Samples
You can also download a PDF copy of this homework assignment.
Instructions: These homework problems will help familiarize you with how we can make inferences concerning the difference between two probabilities (i.e., \(p_1 - p_2\)). For statistical tests state appropriate null and alternative hypotheses, compute the test statistic, compute the p-value, and make a decision/conclusion. Use a significance level of \(\alpha\) = 0.05. For confidence intervals use a confidence level of 95%. The solutions are given at the end.1
Sex Role Stereotypes in Personnel Decisions
Rosen and Jerdee (1974) conducted a randomized experiment to investigate sex role stereotypes in personnel decisions.2 The subjects were 48 male bank supervisors attending a management institute. Each manager was given a hypothetical personnel file and asked if the applicant described in the file should be promoted. The contents of the files were identical except in half of the files the applicant was listed as a man, and in the other half the applicant was listed as a woman. Of the 24 managers who were given the file of a male applicant, 21 recommended promotion, and of the 24 managers who were given the file of a female applicant, 14 recommended promotion. Let \(p_m\) denote the probability that a manager will recommend promotion of the male applicant, and let \(p_f\) denote the probability that a manager will recommend promotion of the female applicant. A statistical test can be used to determine if there is a relationship between the sex of the applicant and the promotion decision using the hypotheses \(H_0: p_m - p_f = 0\) (i.e., the probability of promotion is the same regardless of gender) versus \(H_a: p_m - p_f \neq 0\) (i.e., the probability of promotion is not the same for the two genders). Conduct this statistical test including computing the test statistic, the p-value, and determining whether or not the null hypothesis would be rejected.
Comparison of Two Drugs for Nausea from Chemotherapy
An article in the New England Journal of Medicine described a randomized experiment that investigated the effectiveness of two medications for nausea in patients undergoing chemotherapy treatments for cancer.3 In the experiment, 157 patients were divided at random into two groups. One group of 78 patients were given a standard anti-nausea drug called prochlorperazine, while the other group of 79 patients received delta-9-tetrahydrocannabinol (i.e., THC, the active ingredient in marijuana). Both medications were delivered orally and no patients were told which of the two drugs they were taking. The observed response was whether or not the patient experienced relief from nausea when undergoing chemotherapy. 16 of the patients taking prochlorperazine experienced relief from nausea, while 36 of the patients taking THC experienced relief from nausea. Conduct a statistical test to determine whether or not the probability of a patient experiencing relief from nausea is the same when taking THC versus prochlorperazine. This includes stating the null and alternative hypotheses, computing the test statistic, computing the p-value, and deciding whether or not the null hypothesis is rejected. You may use a one-sided or two-sided test.
Aflatoxicol and Liver Tumors in Trout
Aflatoxicol is a metabolite of Aflatoxin \(\text{B}_1\), a toxin produced by mold that infects cottonseed meal, peanuts, and grains. It sometimes finds its way into freshwater systems. Researchers at the Marine/Freshwater Biomedical Sciences Center at Oregon State University conducted a randomized experiment to investigate the carcinogenic effects of aflatoxicol in rainbow trout (Oncorhynchus mykiss). Tanks of trout embryos were exposed to one of five doses (0.01, 0.025, 0.05, 0.1, or 0.25 ppm) of aflatoxicol for one hour.4 Figure 1 shows the proportion of trout at each dose that developed liver tumors after one year.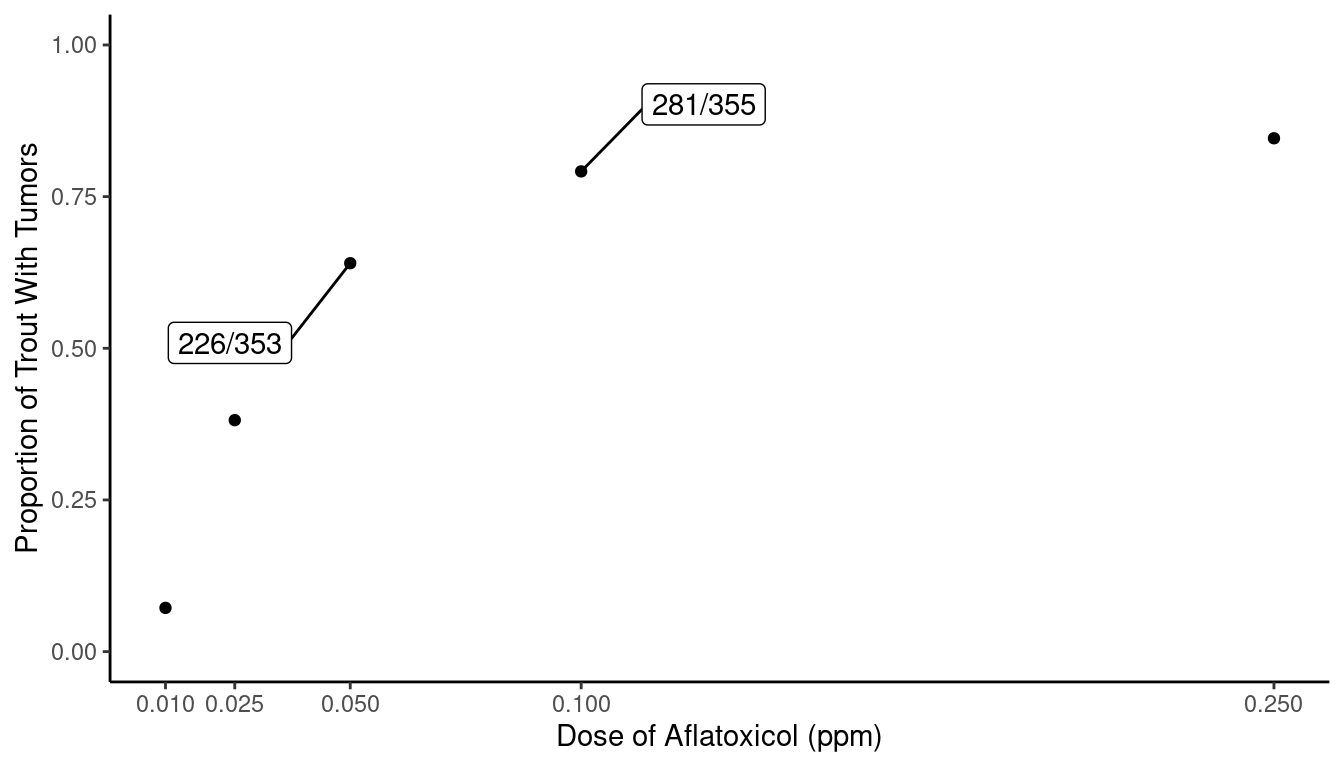
Proportion of rainbow trout with liver tumors one year after exposure to aflatoxicol.
Let \(p_{\scriptsize 0.1}\) denote the probability that a trout will develop liver tumors in one year after exposure to aflatoxicol at a dose of 0.01 ppm, and let \(p_{\scriptsize 0.05}\) denote the probability of the same event but with a dose of 0.05 ppm. Compute an estimate, margin of error, and confidence interval for the difference between these two probabilities — i.e., \(p_{\scriptsize 0.1} - p_{\scriptsize 0.05}\). Note that the sample sizes (353 and 355) are given in the figure, as well as the proportions of trout in each sample (226/353 and 281/355).
Foot Lice Infestation Survey
Researchers at the National Institutes of Hobbit Health (NIHH) are concerned about a possible outbreak of foot lice in the South Farthing.5 They have already made inferences about the incidence of foot lice in the South Farthing based on a simple random sample of 400 Hobbits. But now they want to compare the incidence of foot lice in the South Farthing to that in the North, East, and West Farthings. For this they obtained simple random samples of Hobbits from each of the other Farthings. The sizes of the samples from each Farthing and the number of infested Hobbits in the sample are shown in the table below.| Farthing | yes | no | Total |
|---|---|---|---|
| South | 100 | 300 | 400 |
| East | 20 | 80 | 100 |
| North | 20 | 180 | 200 |
| West | 80 | 320 | 400 |
Let \(p_n\), \(p_s\), \(p_e\), and \(p_w\) denote the probability that a randomly selected Hobbit from the North, South, East, or West Farthing, respectively, has foot lice. Here each probability can also be interpreted as the proportion of all Hobbits in a giving Farthing that a with foot lice. Compute point estimates of differences in the proportion of Hobbits infested with foot lice in the East, North, and West Farthings versus the South Farthing (i.e., \(p_s-p_e\), \(p_s-p_n\), and \(p_s-p_w\)) as well as the associated margins of error and confidence intervals for estimating these quantities.
Sex Role Stereotypes in Personnel Decisions (Solution)
The value of the test statistic is \(z\) \(\approx\) 2.27. For a two-sided test this would yield a p-value of approximately 0.023. Had the researchers used a one-sided test with the alternative hypothesis \(H_a: p_m - p_f \neq 0\) (i.e., the probability of promotion is higher for male applicants) then the p-value would have been approximately 0.011. In either case we would reject the null hypothesis and conclude that there is a statistically significant difference between the proportions of male and female applicants who were recommended promotion. The probability of promotion was not the same for male and female applicants.
Comparison of Two Drugs for Nausea from Chemotherapy (Solution)
Let \(p_t\) and \(p_p\) denote the probabilities that a patient will report experiencing relief from nausea after having been administered THC or prochlorperazine, respectively. Appropriate hypotheses would be \(H_0\!:p_t - p_p = 0\) versus \(H_a\!:p_t - p_p \neq 0\). However if we had anticipated that THC would be more effective so that \(p_t > p_p\) we could also use the one-sided test with hypotheses \(H_0\!:p_t - p_p = 0\) versus \(H_a\!:p_t - p_p > 0\), or a one-sided test with a composite null hypothesis \(H_0\!:p_t - p_p \le 0\). The value of the test statistic is \(z\) \(\approx\) 3.34. For a two-sided test this would yield a p-value of approximately 0.001. For a one-sided test the p-value would be half of the p-value from the two-sided test. In either case we would conclude that the apparent difference in the effectiveness of the two drugs is statistically significant. The probability of experiencing relief does depend on whether the patient was administered THC or prochlorperazine.
Aflatoxicol and Liver Tumors in Trout (Solutions)
The point estimate is just the difference in the proportions, which is approximately 0.15. The margin of error is approximately 0.07. This yields a confidence interval of approximately 0.15 \(\pm\) 0.07.
Foot Lice Infestation Survey (Solution)
The point estimates, margins of error, and confidence intervals are shown in the table below. The margins of error have been rounded to the third decimal place.
| Quantity | Estimate | Margin of Error | Confidence Interval |
|---|---|---|---|
| \(p_s-p_e\) | 0.05 | 0.089 | 0.05 \(\pm\) 0.089 |
| \(p_s-p_n\) | 0.15 | 0.059 | 0.15 \(\pm\) 0.059 |
| \(p_s-p_w\) | 0.05 | 0.058 | 0.05 \(\pm\) 0.058 |
In the solutions the reported values of test statistics and p-values have been rounded some. Rounding was only done for the final reported values. It was avoided in intermediate calculations (e.g., the value of the test statistic used to compute a p-value was not rounded).↩︎
Rosen, B. & Jerdee, J. (1974). Influence of sex role stereotypes on personnel decisions. Journal of Applied Psychology, 59, 9–14.↩︎
Sallan, S. E., Cronin, C., Zelen, M., & Zinberg, N. E. (1980). Antiemetics in patients receiving chemotherapy for cancer: a randomized comparison of delta-9-tetrahydrocannabinol and prochlorperazine. New England Journal of Medicine, 302(3). 135–138.↩︎
There were four tanks of trout embryos per dose for a total of 20 tanks. For simplicity I have combined the data for the tanks at each distinct value of dose. But a more sophisticated analysis would take into account possible variation between tanks.↩︎
Most Hobbits live in a region known as the Shire. It is divided into four regions or Farthings: North, South, East, and West.↩︎