Homework Problem Set 8: Sampling Without Replacement and Estimating Totals
You can also download a PDF copy of this homework assignment.
These problems check your understanding of how to (a) account for sampling without replacement in the calculation of a margin of error and (b) estimation a population total when sampling without replacement. The answers to each problem are given within the problem. You should be able to get the same results.
Note: For simplicity use \(t\) = 2 when computing margins of error and confidence intervals in these problems.
Imagine a warehouse full of 500 boxes. Each box contains one or more widgets. You select a simple random sample without replacement of 100 of these boxes and count the number of widgets in each selected box. In that sample the mean number of widgets per box is 25 widgets and the standard deviation is 5 widgets. Verify that the confidence interval for the mean number of widgets per box for all 500 boxes in the warehouse is approximately 25 \(\pm\) 0.89 widgets per box, and that the confidence interval for the total number of widgets in the warehouse is approximately 12500 \(\pm\) 447.21 widgets.
Anthropologists are trying to estimate the population of a village. They know that the village contains 160 households. The researchers use simple random sampling without replacement to select 16 households and visit each of the selected households. During their visit they determine how many people live in the household. The researchers compute the mean number of people in those 16 households to be 4 people per house, and compute the standard deviation to be 2 people per house. Verify that their estimate of the mean number of people per house in the village is 4 people with a margin of error is about 0.95 people, so that the confidence interval for the mean number of people per house is approximately 4 \(\pm\) 0.95. Also verify that their estimate of the total number of people in the village is 640 people, with a margin of error of about 151.79 people, so that the confidence interval for the total number of people in the village is approxiately 640 \(\pm\) 151.79.
A biologist wants to know the number of eggs that are laid by a female fruit fly. She does not want to count all the eggs, as they are quite small and numerous, so she decides to using sampling to estimate the number of eggs. She gently spreads the eggs on a microscope slide that has had a grid drawn on it such that the slide is divided into 25 squares. The biologist randomly selects 10 different squares, and using a microscope carefully counts the number of eggs on each of the selected squares. The mean number of eggs on those squares is 20 eggs, and the standard deviation is 5 eggs. Confirm that the estimate for the total number of eggs on the entire slide is 500 eggs, with a margin of error of about 61.24 eggs.
Forestry researchers wish to estimate the number of trees in a rectangular-shaped area of forest (see the figure below). The forest has been divided into several rectangular transects. The researchers select some of these transects using simple random sampling without replacement and counts the number of trees in each of the selected transects. Each point in the figure represents a tree, but only those that were in the selected transects were actually counted. The mean number of trees in the sample of transects is 262.6 trees, with a standard deviation of 5.59 trees. Verify that the estimated total number of trees in the forest is 5252 trees with a margin of error of about 87 trees. (Note: The population size and sample size are not explicitly stated, but they can be determined from the figure by counting.)
Archaeologists conducted a survey to estimate the number of artifacts at an archaeological site. See the figure below. The site was divided into smaller square regions using a grid system. Each point in the figure represents an artifact, although these cannot be seen by the archaeologists until the grid square is excavated. The number within each grid square represents the number of artifacts within it. A sample of grid squares was selected using simple random sampling without replacement. A sampled grid square is represented by a solid outline. The archaeologists excavated the selected squares and counted the number of artifacts found therein. The mean number of artifacts per grid square sampled was 10.6 artifacts, and the standard deviation was 3.03 artifacts. Verify that the confidence interval of the total number of artifacts at the site is approximately 1060 \(\pm\) 182 artifacts. (Note: The population size and sample size are not explicitly stated, but they can be determined from the figure by counting.)
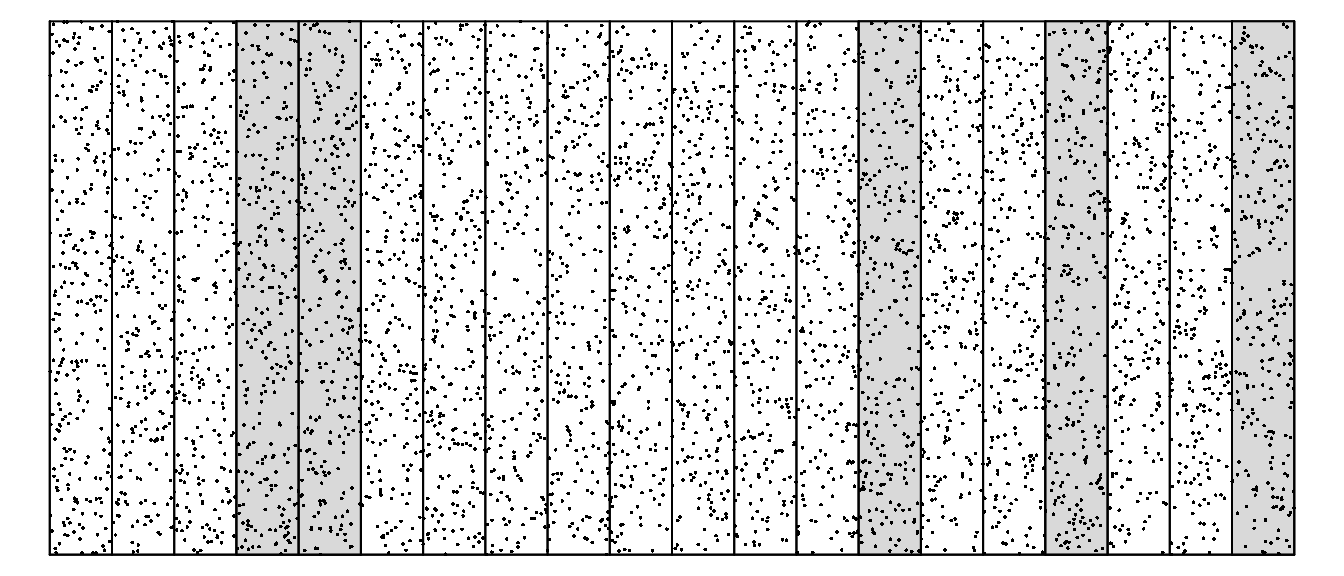
Illustration of transects in a forest. The transects are the tall rectangles. The grey transects represent those transects that were selected using simple random sampling without replacement.
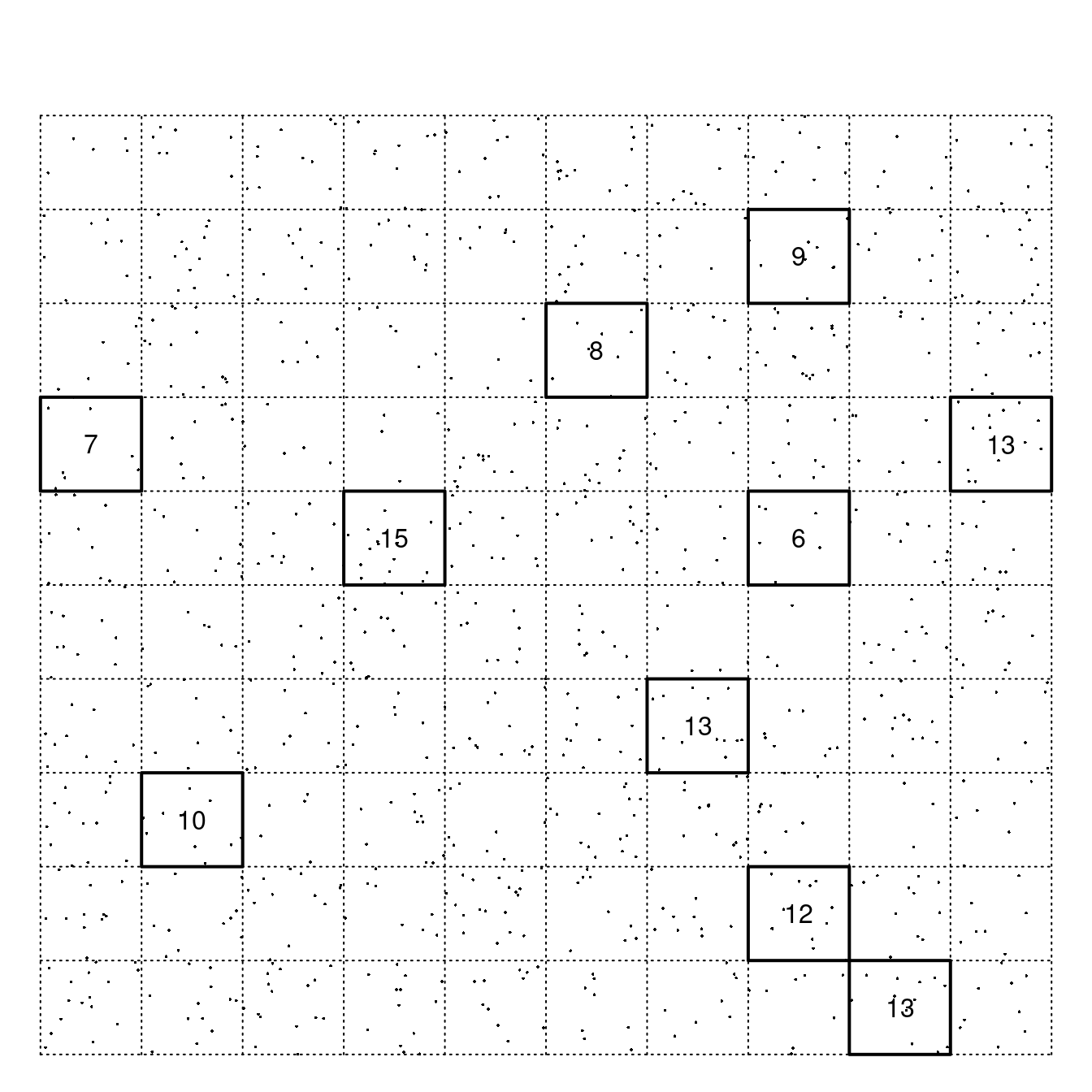
Illustration of an archaeological site with grid. The grid squares with solid outlines were those that were selected using simple random sampling without replacement. The number within each selected rectangular area is the number of artifacts found after excavation of the sampled grid square.